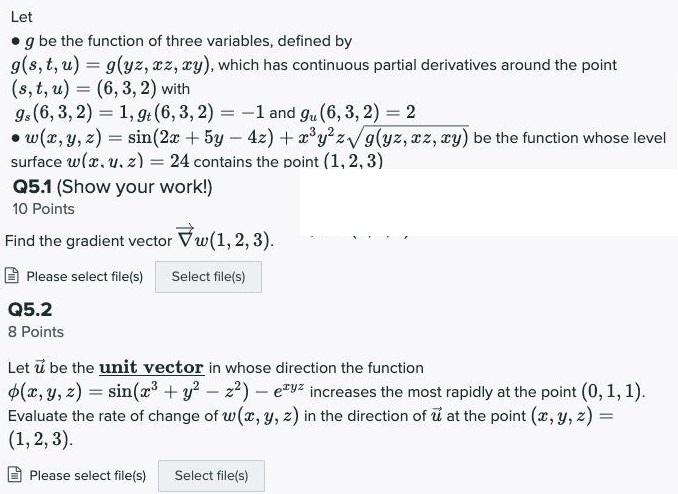
Let g be the function of three variables, defined by g(s, t, u) = g(yz, az, xy), which has continuous partial derivatives around the point (s, t, u) = (6, 3, 2) with g.(6, 3, 2) = 1, 9: (6, 3, 2) = -1 and gu(6, 3, 2) = 2 w(x, y, z) = sin(2x + 5y 4z) + x'y?zVg(yz, xz, cy) be the function whose level surface w(x, u.z) %3D %3D %3D %3! 24 contains the point (1, 2, 3) Q5.1 (Show your work!) 10 Points Find the gradient vector Vw(1, 2,3). Please select file(s) Select file(s) Q5.2 8 Points Let be the unit vector in whose direction the function $(x, y, z) = sin( + y? z?) evz increases the most rapidly at the point (0, 1, 1). Evaluate the rate of change of w(x, y, z) in the direction of u at the point (x, y, z) = (1, 2, 3). Please select file(s) Select file(s)