Question: Q7 First Derivative 4 Points Suppose g is a differentiable function such that it has derivative given by the formula g'(x) = (x -4)(x +

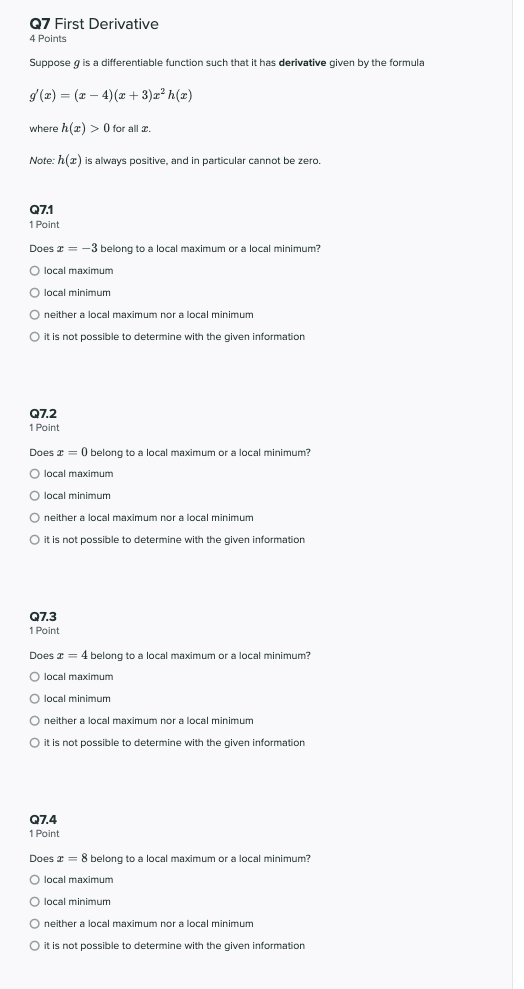
Q7 First Derivative 4 Points Suppose g is a differentiable function such that it has derivative given by the formula g'(x) = (x -4)(x + 3)x3 h(x) where h(r) > 0 for all r. Note: h() is always positive, and in particular cannot be zero. Q7.1 1 Point Does & = -3 belong to a local maximum or a local minimum? O local maximum O local minimum O neither a local maximum nor a local minimum O it is not possible to determine with the given information Q7.2 1 Point Does + = 0 belong to a local maximum or a local minimum? O local maximum O local minimum O neither a local maximum nor a local minimum O it is not possible to determine with the given information Q7.3 1 Point Does + = 4 belong to a local maximum or a local minimum? O local maximum O local minimum O neither a local maximum nor a local minimum O it is not possible to determine with the given information Q7.4 1 Point Does T = 8 belong to a local maximum or a local minimum? O local maximum O local minimum O neither a local maximum nor a local minimum O it is not possible to determine with the given information

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

9. [-/2 Points] DETAILS TANAPCALC10 3.2.036. Find the derivative of the function and evaluate f'(x) at the given value of x. f(x) = 5x + 3. x = 5 5x - 3 f'( X ) = f'(5) = Need Help? Read It 10. [-/1...

Multi step process to 2.2 Section 2.2: Problem 1 Previous Problem (1 point) Use the definition of the derivative (don't be tempted to take shortcuts!) to find the derivative of the function f(x) = 9x...

x 2 V X > O , xleto Typical Application of MVT EEP f(2) = 4 If' ly)1 = 3 find the possible range on . If cat z f ( 6 ) - f (2 ) _ In'len for fial 4. (16 points) doitoml on tards wode (elaioq of) &...

Can you answer Question 4 ( e , f , g , h , i) Content X Bb 1038968 X Bb Derivative X Class Me X Oct28eve X PDE Bernard X M [Ext] 062 X E Cluster A X H04.pdf x + X...

Question 1 Let y=272 3x. 323 5x2. 72r+3 a) Given that In (y) can be written in the form In (y) = In(A)z + In (B) + In (C) z+ In (D). What are the coefficients A, B, C, and D ? A = B = C= D - b) Using...

Suppose f is a differentiable function that satisfies 2xf(x) + cos(f(x) - 1) =9 for all c. If f(4) = 1, what is f (4) ? Answer: f (4) = (You do not need to (nor can you!) find a formula for f()....

__ Find the derivative of the function. G(Z) - (1 - 32) V 23 + 1 Differentiate. G' ( Z) = h(0) = 02 sin(0) Bb Web Assign fall 2021 - Calculus 1 (51) MATH We first note that we can rewrite the...

12. [010.33 Points] DETAILS PREVIOUS ANSWERS SCALCET8 4.1.040. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Find the critical numbers of the function. (Enter your answers as a commaseparated list. Use...

LOL Esports X >MAT1110102-12753202140 (FALL X Homework5 (1).pdf X (1) Home / Twitter X + X -> C O File | C:/Users/Gzhu2/Downloads/Homework5%20(1).pdf ABP G Apps >Dashboard YouTube 3 Lol Esports Home...

Suppose the government is making a $24,000,000,000 expenditure for travel to Mars. If 73% of this amount is spent again, and so on, what is the total effect on the economy? [8.3]

What are the concerns in cash management, and how do cash management ISs help financial managers?

The balance in the Unrealized Gain or Loss- Equity account will a. appear in the stockholders' equity section of the balance sheet b. appear on the statement of comprehensive income c. appear on the...

1. Which of the following methods for uncovering willingness to pay can be used to determine willingness to pay for specific attributes (features) of a product? A. Auction B. Conjoint analysis C....

2. In this chapter, the reader should reflect on the following concepts: Context, winwin, win-lose, ambiguity, mental model, point of reference.

2. In this chapter, the reader should reflect on the following concepts: Patterns, symmetrical relationships, complementary relationships.

1. To provide insight into how setting an overly narrow boundary can give a mes-sage a specific meaning, while setting a wider boundary can give a completely different meaning.