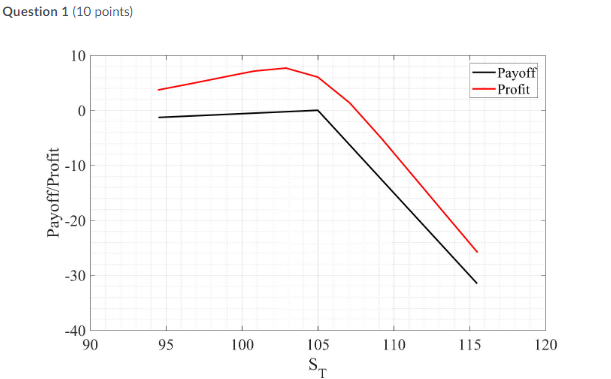
Question 1 (10 points) 10 0 -10 -20 -30 -40 Payoff/Profit 90 95 100 105 ST 110 115 Payoff -Profit 120 Consider a different number of European options, priced with the Black&Scholes Model, with initial stock price SO = 93, strike K = 105, volatility = 0.0688, risk free interest rate = 0.02395, and time to maturity T = 0.083333 years. A combination of long/short positions of calls and/or puts provides the picture attached with the payoff function (in black) and the profit function (in red). What combination of options gives that result? 3 short position(s) in put option(s), 2 short position(s) in call option(s), 2 long position(s) in put option(s), all options with the same strike. 3 short position(s) in put option(s), 2 short position(s) in call option(s), 2 long position(s) in put option(s), 1 short position(s) in call option(s), all options with the same strike. It's not possible to construct the resulting payoff/profit function. 3 short position in a put option. Suppose we observe the prices of 4-year zero-coupon (with a face value of $90.43) and year 2-to-4 forward rate as follows: P(0,4)= $81.9658 and f(2,4)= 0.028593%. Extract the 4-year continuously compounded yields y(0,4): 4.9717% 4.7231% 2.334% 2.4569% Question 1 (10 points) 10 0 -10 -20 -30 -40 Payoff/Profit 90 95 100 105 ST 110 115 Payoff -Profit 120 Consider a different number of European options, priced with the Black&Scholes Model, with initial stock price SO = 93, strike K = 105, volatility = 0.0688, risk free interest rate = 0.02395, and time to maturity T = 0.083333 years. A combination of long/short positions of calls and/or puts provides the picture attached with the payoff function (in black) and the profit function (in red). What combination of options gives that result? 3 short position(s) in put option(s), 2 short position(s) in call option(s), 2 long position(s) in put option(s), all options with the same strike. 3 short position(s) in put option(s), 2 short position(s) in call option(s), 2 long position(s) in put option(s), 1 short position(s) in call option(s), all options with the same strike. It's not possible to construct the resulting payoff/profit function. 3 short position in a put option. Suppose we observe the prices of 4-year zero-coupon (with a face value of $90.43) and year 2-to-4 forward rate as follows: P(0,4)= $81.9658 and f(2,4)= 0.028593%. Extract the 4-year continuously compounded yields y(0,4): 4.9717% 4.7231% 2.334% 2.4569%