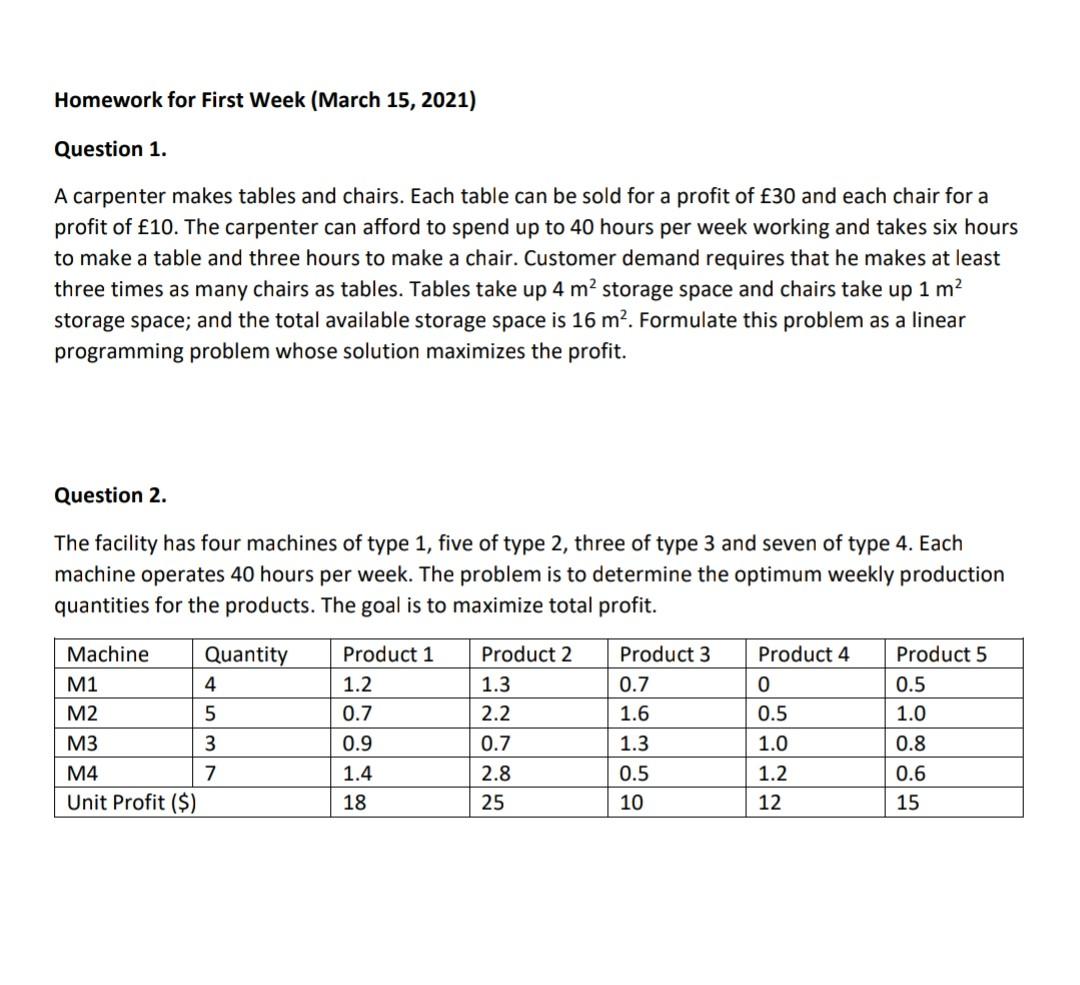
Question 1. A carpenter makes tables and chairs. Each table can be sold for a profit of 30 and each chair for a profit of 10. The carpenter can afford to spend up to 40 hours per week working and takes six hours to make a table and three hours to make a chair. Customer demand requires that he makes at least three times as many chairs as tables. Tables take up 4 m2 storage space and chairs take up 1 m2 storage space; and the total available storage space is 16 m2 . Formulate this problem as a linear programming problem whose solution maximizes the profit. Question 2. The facility has four machines of type 1, five of type 2, three of type 3 and seven of type 4. Each machine operates 40 hours per week. The problem is to determine the optimum weekly production quantities for the products. The goal is to maximize total profit. Machine Quantity Product 1 Product 2 Product 3 Product 4 Product 5 M1 4 1.2 1.3 0.7 0 0.5 M2 5 0.7 2.2 1.6 0.5 1.0 M3 3 0.9 0.7 1.3 1.0 0.8 M4 7 1.4 2.8 0.5 1.2 0.6 Unit Profit ($) 18 25 10 12 15

Homework for First Week (March 15, 2021) Question 1. A carpenter makes tables and chairs. Each table can be sold for a profit of 30 and each chair for a profit of 10. The carpenter can afford to spend up to 40 hours per week working and takes six hours to make a table and three hours to make a chair. Customer demand requires that he makes at least three times as many chairs as tables. Tables take up 4 m2 storage space and chairs take up 1 m2 storage space; and the total available storage space is 16 m. Formulate this problem as a linear programming problem whose solution maximizes the profit. Question 2. The facility has four machines of type 1, five of type 2, three of type 3 and seven of type 4. Each machine operates 40 hours per week. The problem is to determine the optimum weekly production quantities for the products. The goal is to maximize total profit. Product 1 1.2 0.7 Machine Quantity M1 4 M2 5 M3 3 7 Unit Profit ($) Product 2 1.3 2.2 0.7 2.8 25 Product 3 0.7 1.6 1.3 0.5 10 Product 4 0 0.5 1.0 1.2 12 Product 5 0.5 1.0 0.8 0.6 15 M4 0.9 1.4 18