Question $1$:

A lumber company operates three processing facilities that require logs on a weekly basis for

lumber production. The minimum weekly demand for logs at each facility is as follows:

Facility A: $600$m$^(3)$

Facility B: $500$m$^(3)$

Facility C: $400$m$^(3)$

The company sources its logs from two forest zones:

Forest Zone $1$: Can supply up to $900$m$^(3)$ of logs per week.

Forest Zone $2$: Can supply up to $700$m$^(3)$ of logs per week.

To streamline operations, the company plans to establish a central log sorting yard. This sorting

yard will receive logs from the forest zones and distribute them to the processing facilities. The

potential locations for the sorting yard are at Facility A$,$ Facility B$,$ or Facility C$.$ The construction

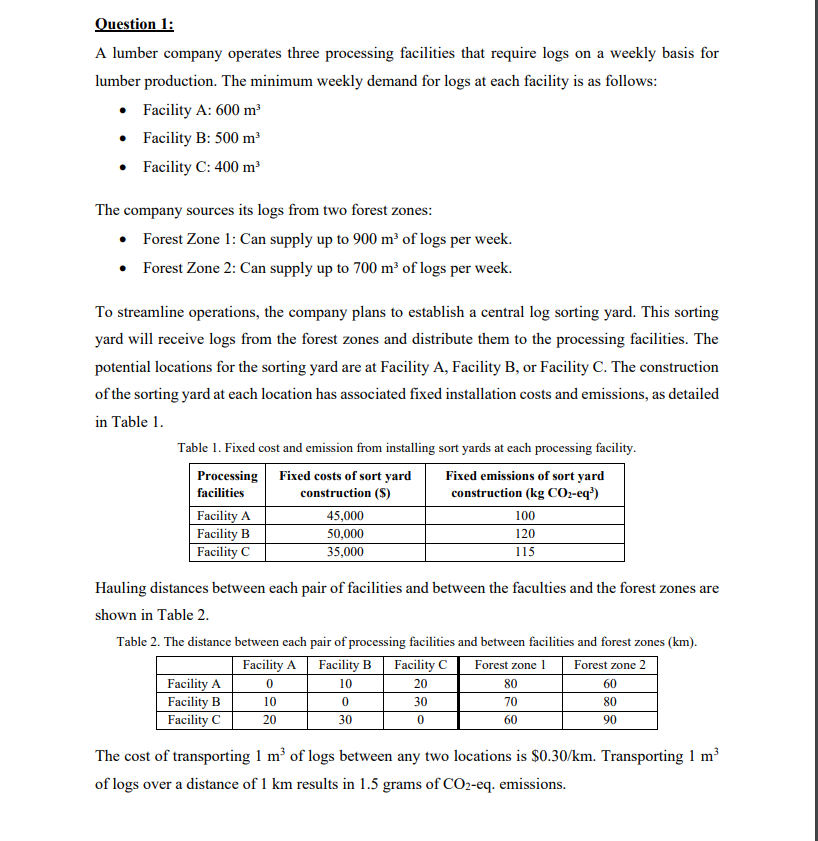
of the sorting yard at each location has associated fixed installation costs and emissions, as detailed

in Table $1.$

Table $1.$ Fixed cost and emission from installing sort yards at each processing facility.

Hauling distances between each pair of facilities and between the faculties and the forest zones are

shown in Table $2.$

Table $2.$ The distance between each pair of processing facilities and between facilities and forest zones $($ km $).$

The cost of transporting $1$m$^(3)$ of logs between any two locations is $$0\mathrm{.}30//$km$.$ Transporting $1$m$^(3)$

of logs over a distance of $1$ km results in $1\mathrm{.}5$ grams of CO$\_(2)-$eq$.$ emissions.

Part A: Develop an optimization model to determine the optimal location of the sort yard that minimizes the total transportation and sort yard construction cost. Solve the model using the Excel Solver. Define the decision variables, objective function and constraints clearly. Explain your results.

Part B: Modify the model you developed in Part A to minimize the total emissions from transportation and construction of the sort yard. Solve the model using the Excel Solver. Define the decision variables, objective function and constraints clearly. Explain your results and compare them with Part A$.$

Part C: Suppose the logging company aims to simultaneously consider the objectives of minimizing the total cost and emissions. For each objective, the company has set specific goals, which are as follows:

$$ The cost goal is the minimum cost found in Part A$.$ The company wants to minimize the overachievement of the cost goal.

$$ The emission goal is set at $1\mathrm{.}5$ times the minimum emissions determined in Part B$.$ The company aims to maintain emissions as closely aligned as possible with this emission goal. Assuming equal priority for both goals, develop a goal programming model aimed at minimizing the overall deviations from the aforementioned goals. Clearly outline the goals, decision variables, the objective function, and the constraints of the model. Use Excel Solver to solve the model. Report your results and compare them with Part A and Part B$.$

Part D: Suppose that achieving the cost goal is five times as important as achieving the emission goal. Develop the goal programing model and solve it using Excel Solver. Compare your results with those in Part C$.$