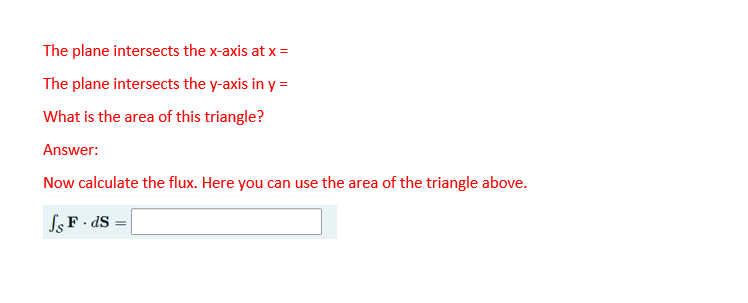
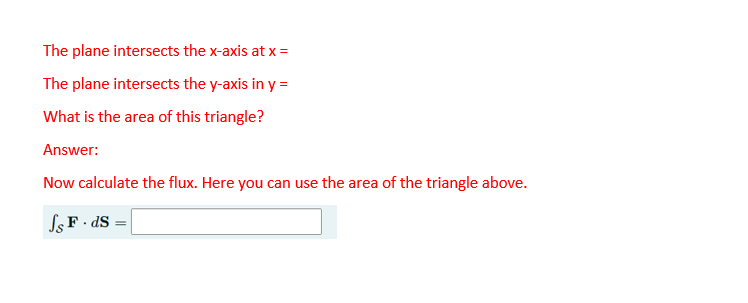
Question 1 A plane 5 is given at the part of the plane 1: + 11; + 12 = 1 in the first octane (at, v, zero}. The orientation of the surface is given so that the zcoordinate of the unit 1'- normal vector is positive at any:r point on the surface. Remember that for a surface 5 described with an equation 2 = f {:c v} we know that =i4 _% a 2 a 2 1+(s') +(sf') 1 where the sign depends on the orientation, as well as that delivssgfm Now calculate the element d5 = N53- Note! N\" is a vector so your answer will be in the form [21; 43!, 53] dxdy, then write onlv [2x. 43;. 52] and not dxdy. We now want to calculate the flux of the vector eld _E Lap3'5: 3; 21] through the surface 5. 1 Now the question is which area in the 531 plane we should integrate over. We can see that it is a triangle T with corner edges at the origin, as well as at the points where the plane intersects the xaxis and where it intersects the vaxis. At what points does the plane intersect the x and v axes? The plane intersects the xaxis at x = The plane intersects the 'faxis in yr = What is the area of this triangle? Answer: New calculate the flux. Here 1,Inau can use the area of the triangle above. M43