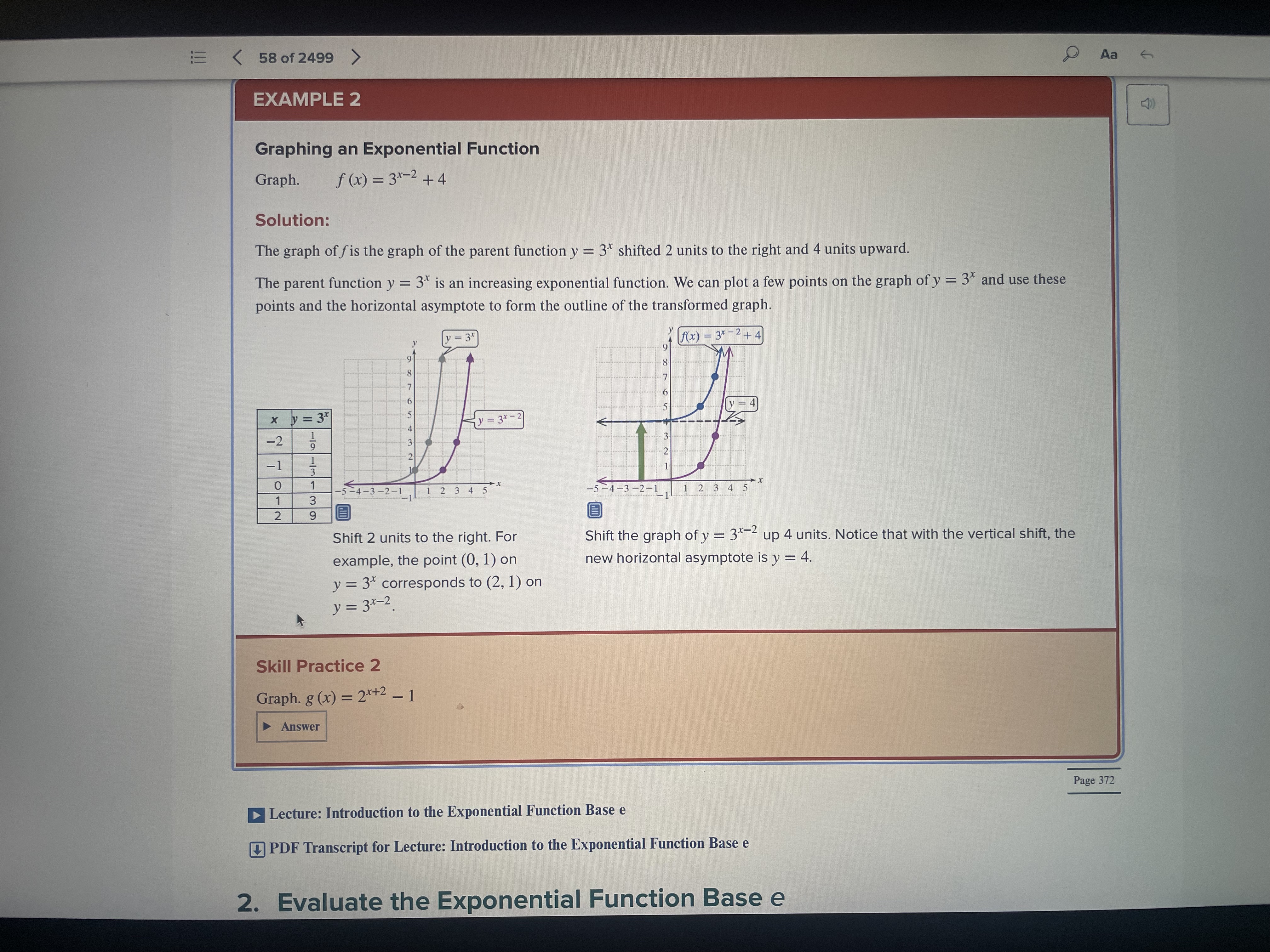
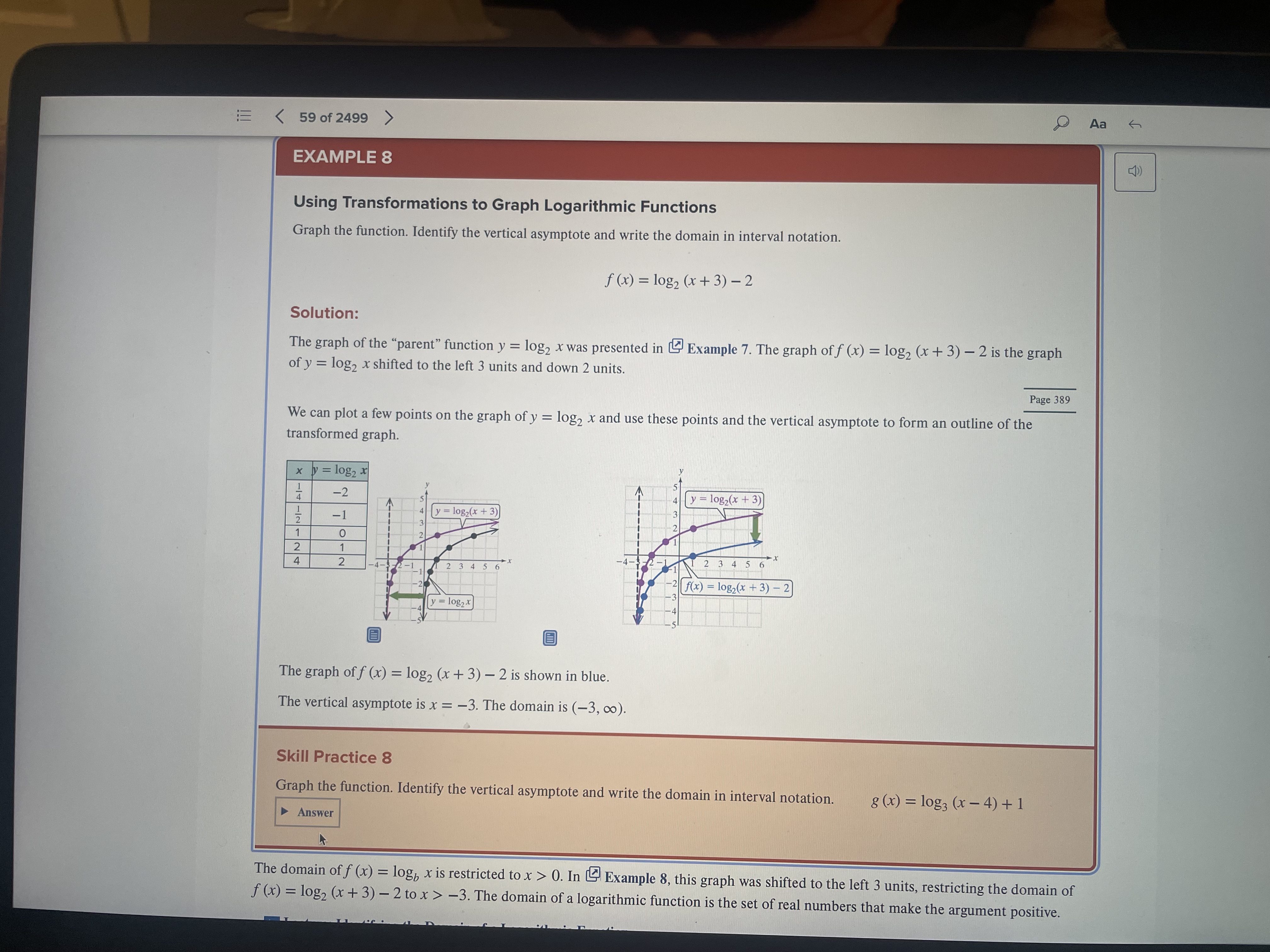
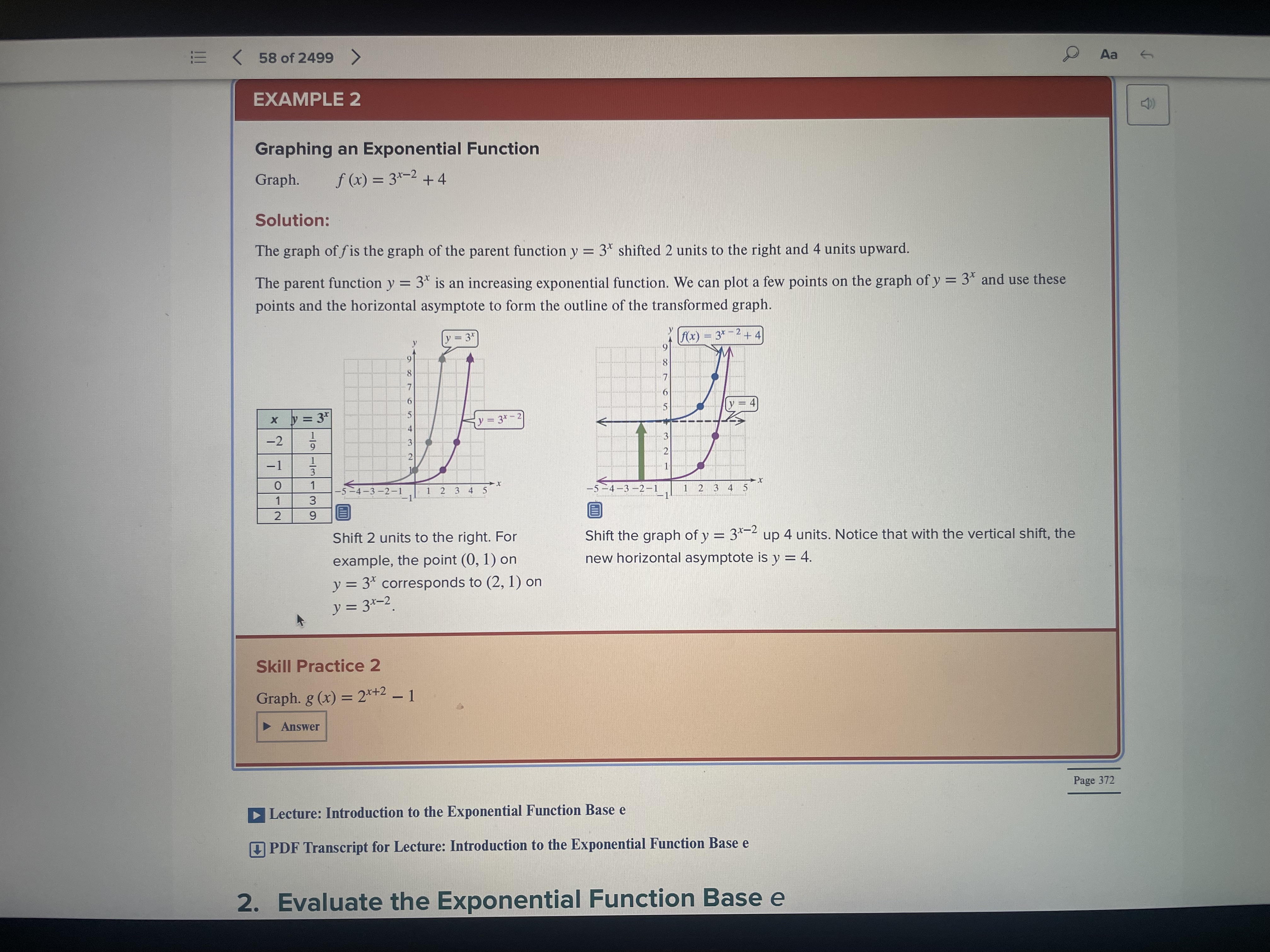
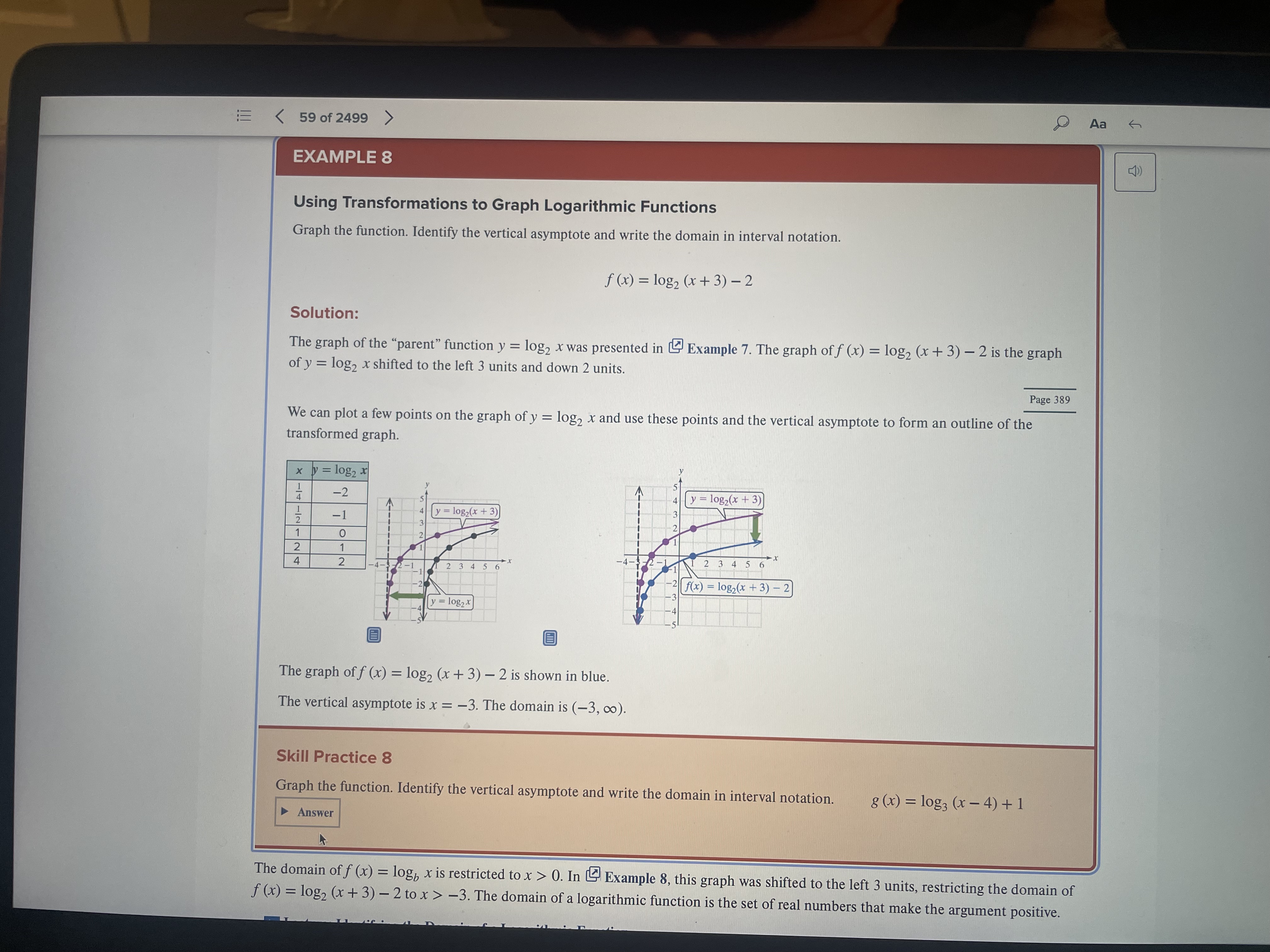
Question 1: Answer. Given the transformed function y = f(x ~ 1) + 3 , answer the following, showing your calculations: {a} Suppose the parent function is f(x) = 9.". Transform the parent function points it}, 1) and {1, e) as shown in Example 2 on p. 371. Use those points to help you sketch an accurate graph of the transformed function. Show the asymptote and compute any intercepts. Write the domain and range using correct set notation. {8pts} {[3} Suppose the parent function is f(x) = logc. Transform the parent function points (1, 0) and (10, 1} as shown in Example 8 on p. 388. Use those points to help you sketch an accurate graph the transformed function. Show the asymptote and compute any intercepts. Write the domain and range using correct set notation. (Sptsi Question 2: Create. Identify 3 characteristics of inverse functions. Create a non-linear function {restricting the domain is OK) that you believe has an inverse. Show a graph of your function and explain why it has an inverse. {lets} We. Search the internet for bank interest rates. Create a scenario where you decide to deposit a lump Sum of money into a savings account. Be creative! Make sure to include the interest rate, how often the money will be compounded (annually, quarterly, monthly, daily or continuously), how much is to be invested and how long you will leave the money in the bank. {pts} Aa EXAMPLE 2 Graphing an Exponential Function Graph. f ( x ) = 3*-2+4 Solution: The graph of fis the graph of the parent function y = 3" shifted 2 units to the right and 4 units upward. The parent function y = 3" is an increasing exponential function. We can plot a few points on the graph of y = 3" and use these points and the horizontal asymptote to form the outline of the transformed graph. f(x) - 37 2 +4 x y = 3* y = 3x-2 -2 -1 0 -5-4-3-2-1 5-4-3 -2-1 1 3 1 2 3 4 5 N - Shift 2 units to the right. For Shift the graph of y = 3"- up 4 units. Notice that with the vertical shift, the example, the point (0, 1) on new horizontal asymptote is y = 4. y = 3* corresponds to (2, 1) on y = 3*- 2 Skill Practice 2 Graph. g (x) = 2*+2 - 1 Answer Page 372 Lecture: Introduction to the Exponential Function Base e PDF Transcript for Lecture: Introduction to the Exponential Function Base e 2. Evaluate the Exponential Function Base e Aa EXAMPLE 8 Using Transformations to Graph Logarithmic Functions Graph the function. Identify the vertical asymptote and write the domain in interval notation. f (x) = 1082 (x+ 3) -2 Solution: The graph of the "parent" function y = log2 x was presented in & Example 7. The graph of f (x) = log2 (x + 3) - 2 is the graph of y = 10g2 x shifted to the left 3 units and down 2 units. Page 389 We can plot a few points on the graph of y = log2 x and use these points and the vertical asymptote to form an outline of the transformed graph. x y = 10g2 X -2 W Au y - log2(x + 3) y = log,(x + 3) D N - NI - Al - 12345 6 2 f(x) - 1082(x + 3) - 2 y = 10g2 X The graph of f (x) = log2 (x + 3) - 2 is shown in blue. The vertical asymptote is x = -3. The domain is (-3, co). Skill Practice 8 Graph the function. Identify the vertical asymptote and write the domain in interval notation. 8 (x ) = 10g3 (x - 4) + 1 Answer The domain of f (x) = log, x is restricted to x > 0. In L Example 8, this graph was shifted to the left 3 units, restricting the domain of f (x) = 10g2 (x+ 3) -2 to x > -3. The domain of a logarithmic function is the set of real numbers that make the argument positive