Question $1$

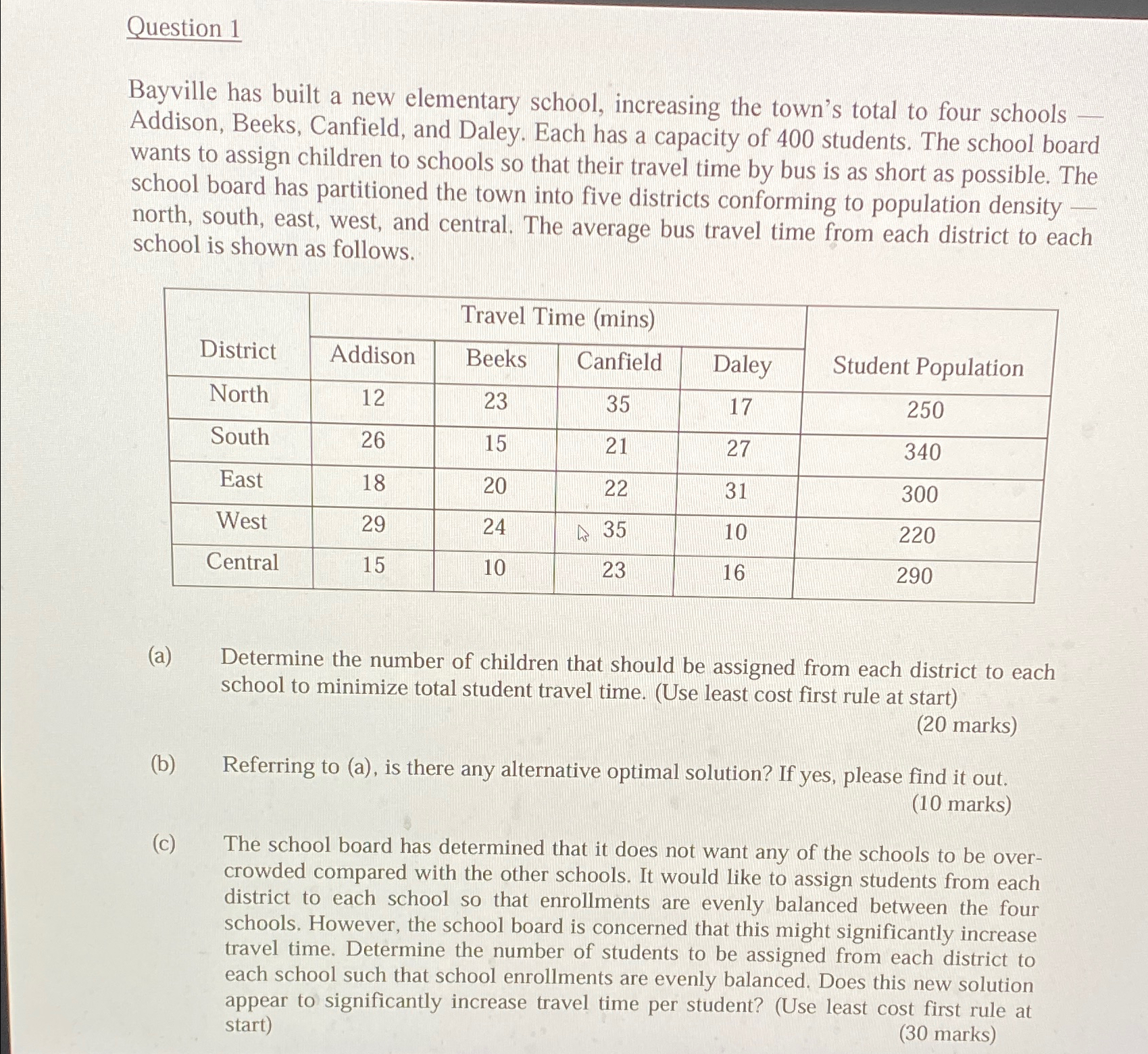
Bayville has built a new elementary school, increasing the town's total to four schools Addison, Beeks, Canfield, and Daley. Each has a capacity of $400$ students. The school board wants to assign children to schools so that their travel time by bus is as short as possible. The school board has partitioned the town into five districts conforming to population density north, south, east, west, and central. The average bus travel time from each district to each school is shown as follows.

$\backslash$table$[[$District$,$Travel Time $($mins$),$Student Population$],[$Addison$,$Beeks,Canfield,Daley$],[12,23,35,17,340],[$South$,26,15,21,27,300],[$East$,18,20,22,31,220],[$West$,29,24,35,10,290],[$Central$,15,10,23,16,]]$

$($a$)$ Determine the number of children that should be assigned from each district to each school to minimize total student travel time. $($Use least cost first rule at start$)$

$(20$ marks$)$

$($b$)$ Referring to $($a$),$ is there any alternative optimal solution? If yes, please find it out.

$(10$ marks$)$

$($c$)$ The school board has determined that it does not want any of the schools to be overcrowded compared with the other schools. It would like to assign students from each district to each school so that enrollments are evenly balanced between the four schools. However, the school board is concerned that this might significantly increase travel time. Determine the number of students to be assigned from each district to each school such that school enrollments are evenly balanced. Does this new solution appear to significantly increase travel time per student? $($Use least cost first rule at start$)$

$(30$ marks$)$