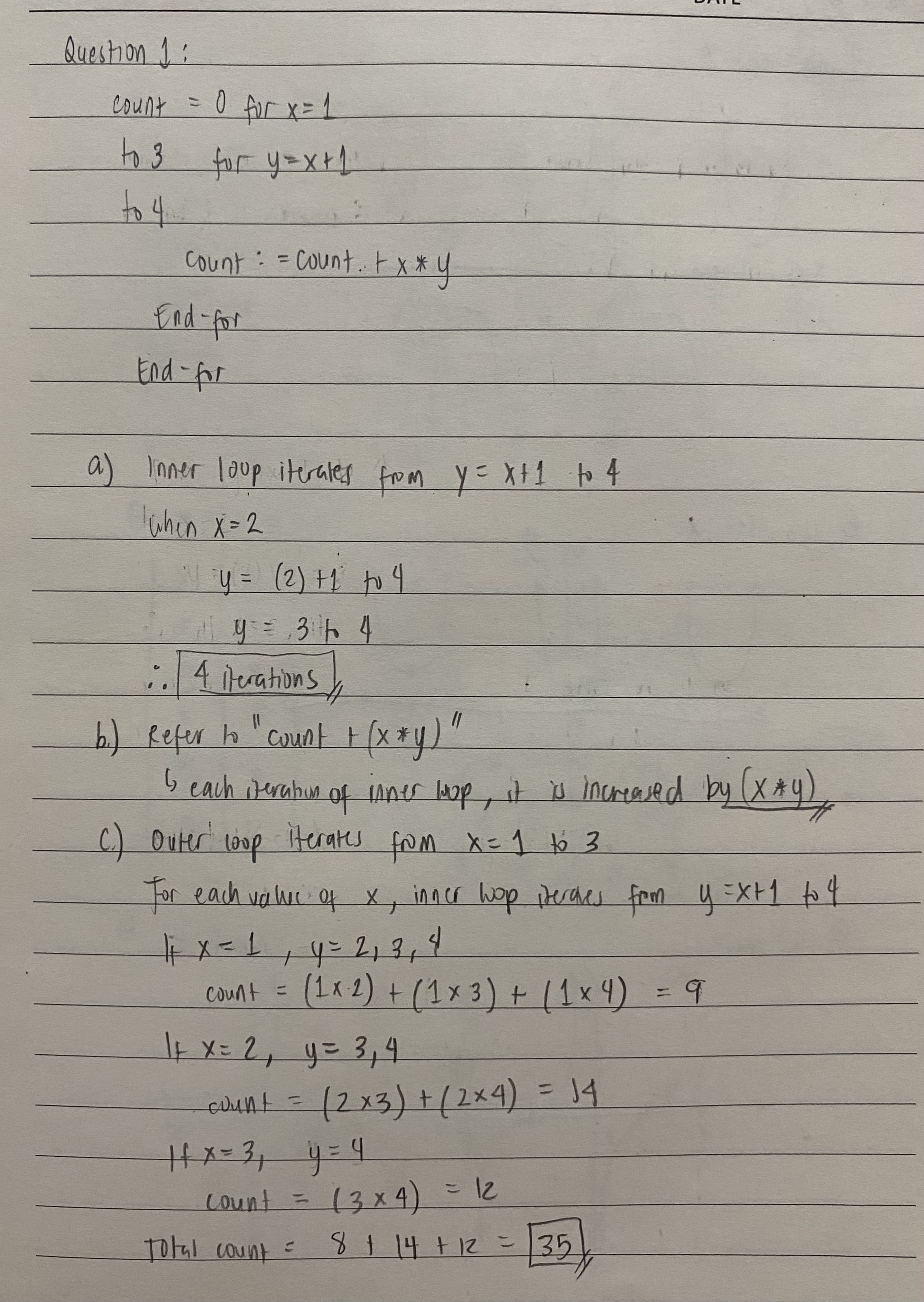
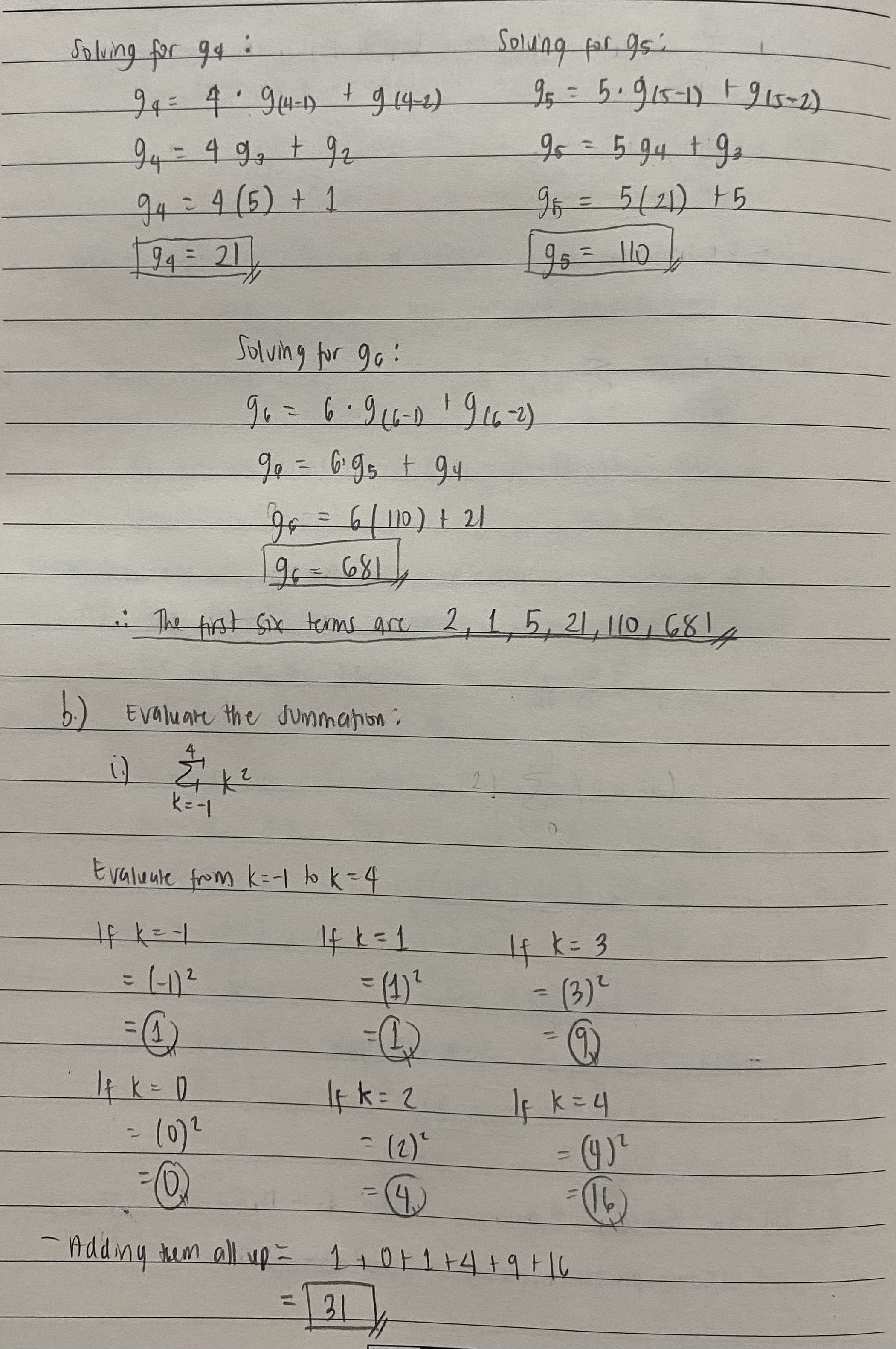
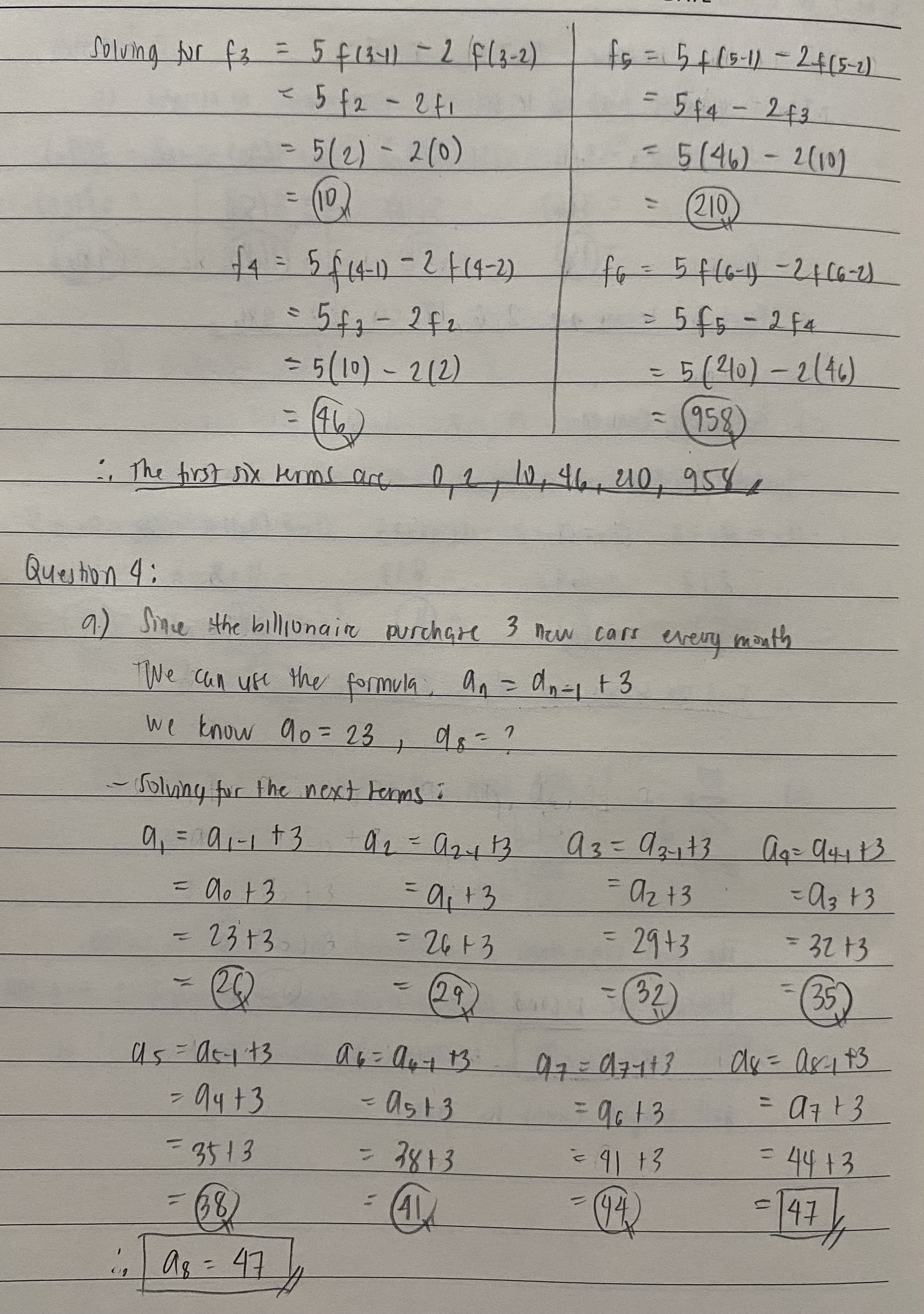
Question 1: Consider the following pseudocode fragment: count: = 0 for x = 1 to 3 for y = x + 1 to 4 count: = count + x * y End-for End-for a) For the iteration of the outer loop where x=2, how many times does the inner loop iterate? b) How many times is the variable "count" increased? c) What is the final value of "count"?Question 2: For each of the sequences described below, indicate which of the following properties describes the sequence, keeping in mind that the sequence may have more than one of the properties, or none of the properties: . Increasing . Decreasing Non-increasing . Non-decreasing a) an = n' - 3n, for n >=1 b) an = n2 - 2n, for n>=1 c) Give numerical values for the following summations. E (2) - 1) [2- (+1) 2 Question 3: a) Give the first six terms of the following sequence. gi = 2 and g2 =1. The rest of the terms are given by the formula ga = no gn-1 + gn-2. b) Evaluate the following summations. 1) _ 20 (2 + 3k ) c) Give the first six terms of the following sequences. fi = 0, f2 = 2, and fo = 5. fn-1 - 2. fn-2 for n23.Question 4: a) A Silicon Valley billionaire purchases 3 new cars for his collection at the end of every month. Let a. denote the number of cars he has after n months. Let ao = 23. What is as? (5 b) Give the first six terms of the following sequences. You can assume that the sequences start with an index of 1. A geometric sequence in which the first value is 2 and the common ratio is 3. ) Give the first six terms of the following sequences. You can assume that the sequences start with an index of 1. An arithmetic sequence in which the first value is 2 and the common difference is 3. d) Indicate whether the following equality is true and justify your answer: 100 .3 _ 100 .3 j=07 e j=1 Question 5: a) Express sums using summation notation 22 + 23 + 24+ 25 + 26 + 27 + 28 b) Let {su} be a geometric sequence that starts with an initial index of 0. The initial term is 16 and the common ratio is 1/2. What is s3? ) Consider the arithmetic sequence: 7, 4, 1, .... What is the next term in the sequence? Question 5: a ) Express in summation notation . 2 ( F 2 5 } 2" + 25 + 26 + 27+28 Notice that you are simply adding 2 from x = 2 to x = 8 8 Z * = 2 p . ) Geometric sequence : f sny initial term = 1b r = 1/ 2 Use formula Sn = arn " where a = initial term . - solving for $3 : n = 3 8 3 = 16 ( 12 ) 53 = 2 C. ) 7, 4, 1... what Is the next term : ? Notice that 4-7 2 4 1- 4 = (3 - 3 the common difference Is - 3 - Sowing for the next term ,Question 1 : count = 0 for * = 1 to 3 for y = x + 1 to 4 count : = count. . + x * 4 End - for End - for a ) Inner loup iterates from y = x+ 1 to 4 When x = 2 y y = (2 ) +1 to 4 y = 3 1 4 4 iterations b. ) Refer to count + ( x * y ) " I each iteration of inner wop, it is increased by ( x * 4 ) ( . ) outer loop iterates from x = 1 to 3 For each value of x , inner wop perales from 4 = *+ 1 to 4 *FX = 1 , 4 = 2, 3 , 4 count = ( 1 x 2 ) + ( 1 x 3 ) + ( 1 * 4 ) = 9 IF X = 2 , y = 3, 4 count = (2 x 3 ) + ( 2 x 4 ) = 14 1 x = 3 4 = 4 count = ( 3 x 4 ) = 12 Total count = 8 1 14 + 12 - 35Queshan 2 : al an = n 2 - 3n , for 1 21 ") Derivative is the slope of your equation . The refore , you will know From there if it is increasing / decreasing if it has a positive / negative slope , respectively Therefore , take the denvalve of the equation 9'n = 20 - 3 ( Power rule ) Equate to zero 0 = 20 - 3 3 = 2n 1 = 3 Remember , we are evaluating for 1 2 1. Meaning your Values of n are only 1 , 2, 3 .. and so on . These values are greater than 3 / 2 :. n 7 3 /2 Thus , an is positive & the sequence Is Increasing athr n = 3/2 . That's why it Is non decreasing b. ) a A = 1 2 - 20 , for n 2 1 Take the denvalive , 9'n = 2n - 2 ( Power rule ) 0 = 20 - 2 n = 2 i. n 7 1 Thus , an is positive , it is increasing as well as increasing after he 1 . That's why The sequence is increasing and non-decreallySMTWTFS DATE 1 = 2 J = 0 Evaluate from j = 2 to j=5 Evaluate from 1= 0 to j= 2 IF ] = 2 If j = 0 = 2 (2 ) - 1 = ( 0 + 1 ) 2 =(3 1) = 1 if j = 3 I F j = 1 = 2 (3) - 1 = ( 1 + 1 ) 2 = 5 , = 4 If j = 9 ( F j = 2 = 214 ) - 1 1 = ( 21 1 ) 2 - 9 - Adding them all up, = 2(5)-1 = 1+4+9 14 Adding them all up , = 3+5+7+8 = 124 Question 3 : 4) gn = n . 9 n -| + 9n-2 where 9, = 2 and 9 2 = 1 solving for gg , 1 = 3 Substitute q , and go values 93 = 3 . 9 (3 -1 + 913- 2) 9 3 = 3 / 1 ) + 2 97 = 3 . 92 + 9 , 931 = 5 ( Repeat the same proves for the next teams)solving for 9q : Solving for go . 9 4 : 4 ' 9 (4-1 + 9 14-2) 9 5 = 5 . 9 15 - 17 + 9 15 -2) 9 4 = 4 9, + 9z 95 = 5 94 + 92 94 = 4 (5 ) + 1 95 = 5 / 21 ) +5 94 = 21 1 95 = 110 Solving for go ! 9 6 = 6 . 9 ( 6 - D + 9 (6 -2 ) 95 = 6 /110 ) + 21 94 - 681 " The first six terms are 2 , 1 5, 21, 110 , 681, b . ) Evaluate the summation: K= - 1 Evaluate from K= -1 to k = 4 If K = - 1 If k = 1 f * = 3 = 1 -1) 2 ( 1 ) 2 = (3)2 If K = D If k = 2 F K = 4 = (0 ) 2 F ( 2 ) " ( 4) 2 (0) = ( 4 ) 16 ) - Adding them all up = 1 + 0 + 1 + 4 + 9 +1 6 31DATE if ) 5 ( 213 * ) - fsince 20 is a very large number , we can 1= 0 split the summation in 2 parts ) 200 200 1=0 7 For summation of a constant number that is simply = an where 1 = any constant and n = no. of terms. solving for 2 2, a -2 A = 201 ( since there art zottcross from A-20) 1=0 . = 2 (201 ) 402 For summation of linear term k, simply use the formula : n ( n+1 ) where n is the no . of terms 2 wo solutAy for 21 3K . 120 3 * + 1 = 201 izo = 3 201 ( 201+1 ) ) 2 = 60 300) - Adding them up = 402 + 603 0 0 60702 ( ) fn = 5 fin-1 - 2 { ( - 2) where fi = 0 , f 2 = 2 , n > 3 ( same procell ( explanation from them 3 . G )Solving for (3 = 5 f ( 3-11 - 2 f ( 3 - 2 ) fo =15 + ( 15-11 - 24(5-2)