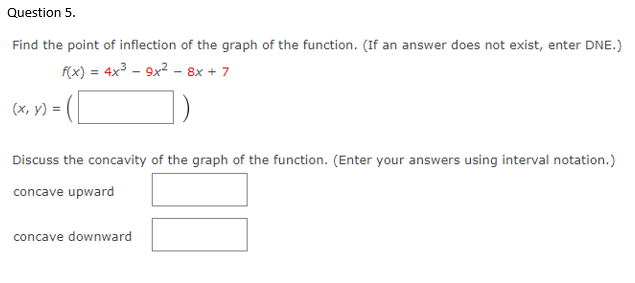
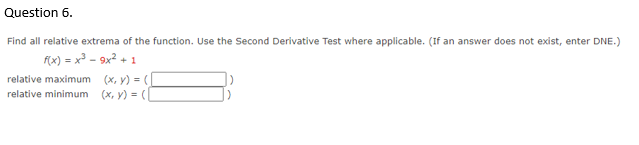
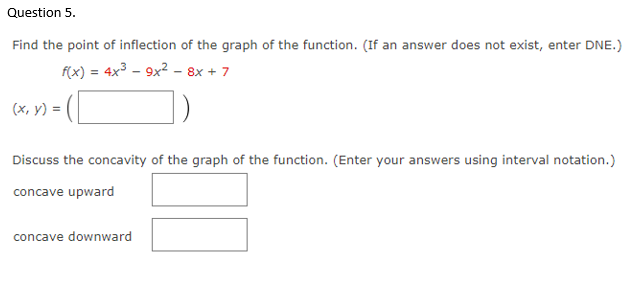
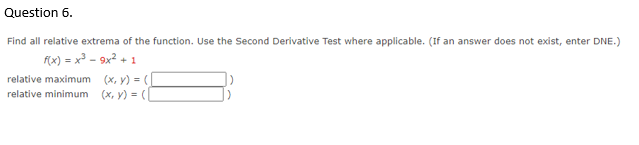
Question 1. Determine the open intervals on which the graph is concave upward or concave downward. (Enter your answers using interval notation. If an answer does not exist, enter ONE.) 7(x) = 27x- x2 concave upward concave downward Question 2. Determine the open intervals on which the graph is concave upward or concave downward. (Enter your answers using interval notation. If an answer does not exist, enter DIME.) (xx - px concave upward concave downward Question 3. Find all relative extrema of the function. Use the Second-Derivative Test when applicable. (If an answer does not exist, enter DNE.) f(x) = x4 - 8x3+ 2 relative maximum (x, y) = relative minimum (x, y) = Question 4. Determine the open intervals on which the graph is concave upward or concave downward. (Enter your answers using interval notation. If an answer does not exist, enter ONE.) =-x + 15x - 4 concave upward Concave downwardQuestion 5. Find the point of inflection of the graph of the function. (If an answer does not exist, enter DNE.) f(x) = 4x3 - 9x2 - 8x + 7 ( x, V ) = Discuss the concavity of the graph of the function. (Enter your answers using interval notation.) concave upward concave downwardQuestion 6. Find all relative extrema of the function. Use the Second Derivative Test where applicable. (If an answer does not exist, enter DNE.) (x) = x - 9x2 + 1 relative maximum (x, y) = ( relative minimum (x, y) = (