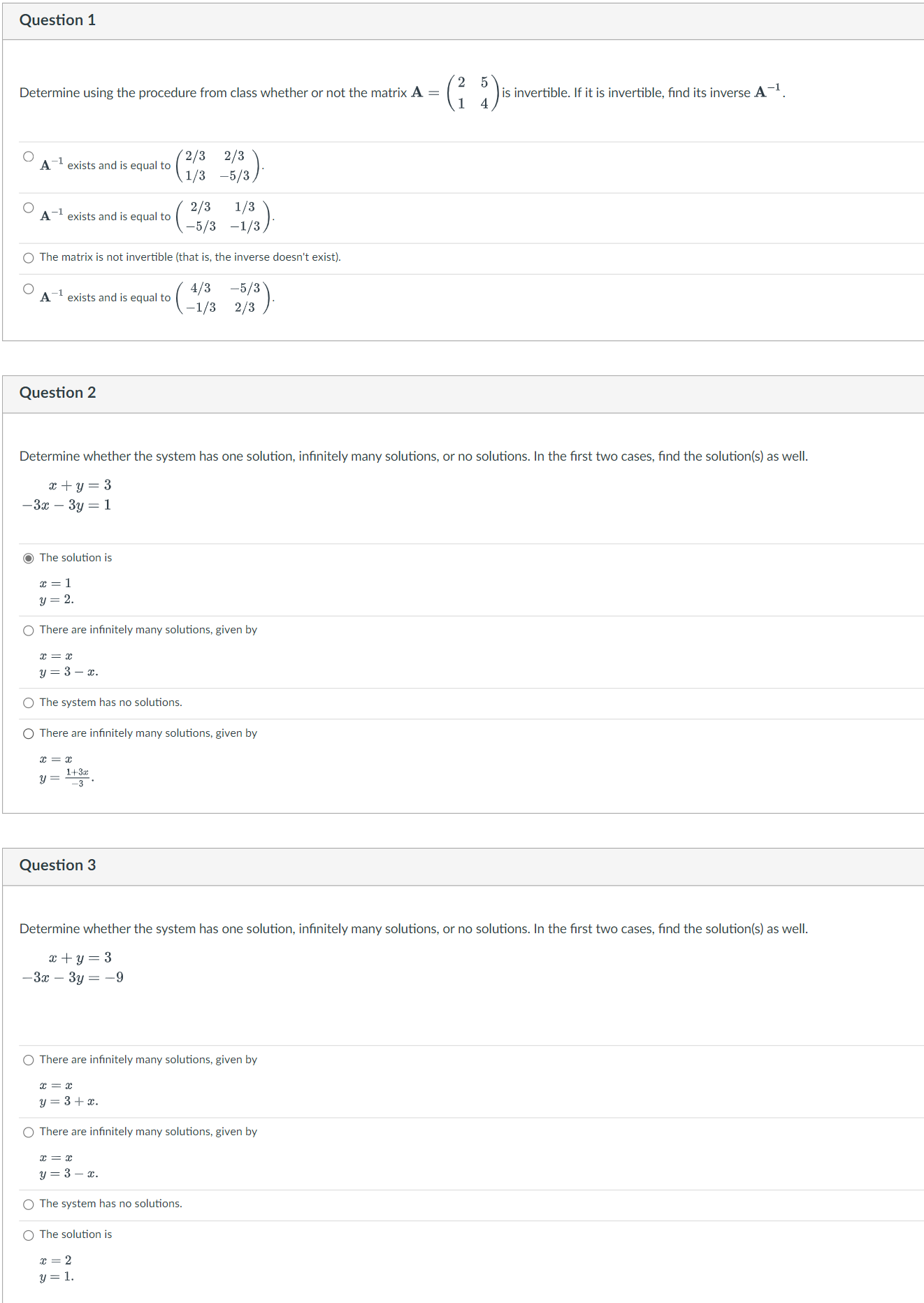
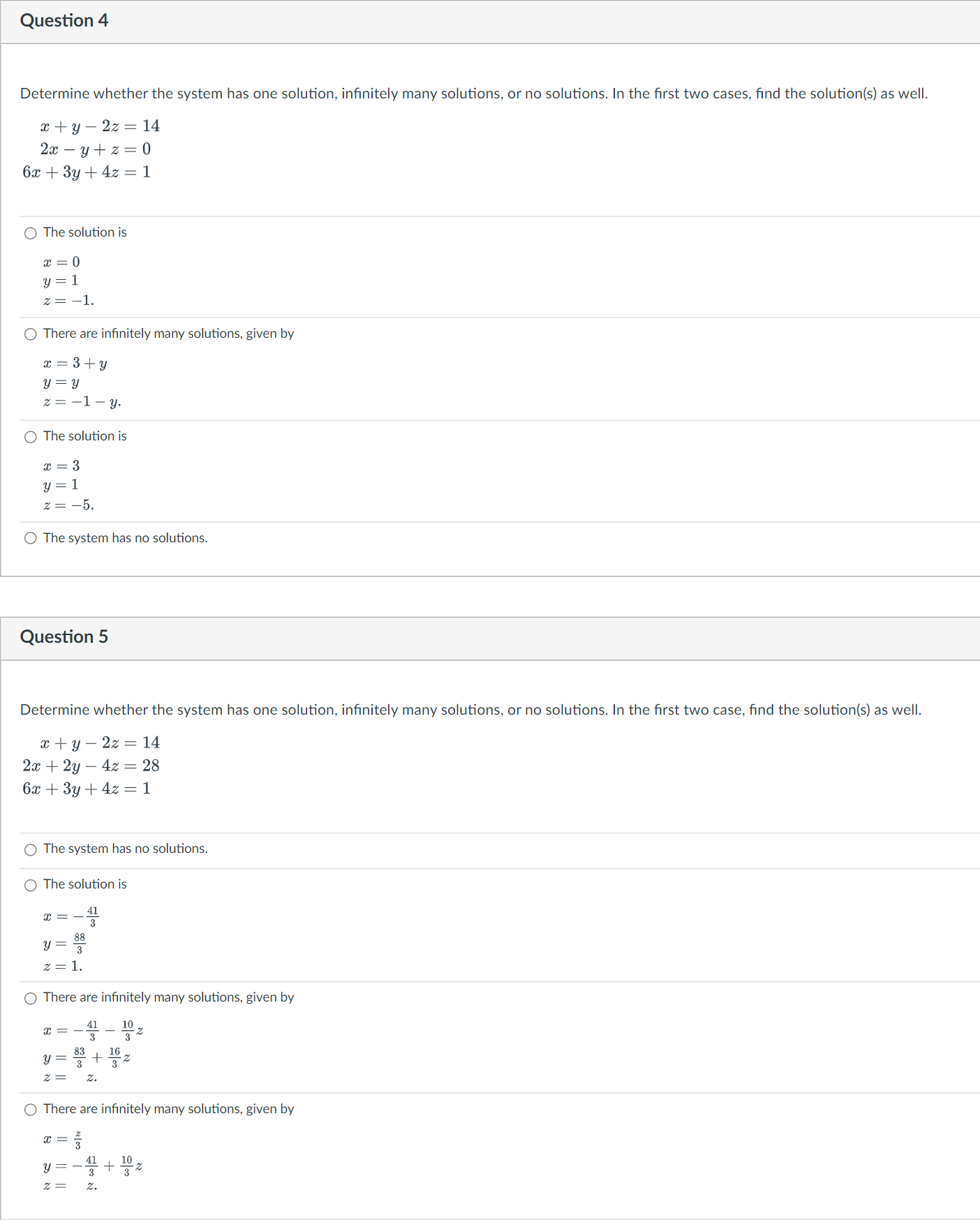
Question 1 Determine using the procedure from class whether or not the matrix A is invertible . If it is invertible, find its inverse A -1 . A 1 exists and is equal to ( 2/3 2/3 1/3 -5/3) A exists and is equal to 2/3 1/3 -5/3 -1/3/ The matrix is not invertible (that is, the inverse doesn't exist). A-1 exists and is equal to (4/3 -5/3) (-1/3 2/3 Question 2 Determine whether the system has one solution, infinitely many solutions, or no solutions. In the first two cases, find the solution(s) as well. cty = 3 -3x - 3y = 1 O The solution is C=1 y = 2. There are infinitely many solutions, given by x = x y = 3 - x. O The system has no solutions. O There are infinitely many solutions, given by c = C y = 1ta Question 3 Determine whether the system has one solution, infinitely many solutions, or no solutions. In the first two cases, find the solution(s) as well. xty=3 -3x - 3y = -9 O There are infinitely many solutions, given by y = 3+2. O There are infinitely many solutions, given by x = X y = 3 - 2. O The system has no solutions. The solution is 2 = 2 y=Question 4 Determine whether the system has one solution, infinitely many solutions, or no solutions. In the first two cases, find the solution(s) as well. cty - 2z = 14 2x - y+ z =0 6x + 3y + 4z = 1 O The solution is x=0 y =1 2 = - O There are infinitely many solutions, given by c= 3+y y = y z = -1-y. O The solution is x = 3 y =1 2 = -5 O The system has no solutions. Question 5 Determine whether the system has one solution, infinitely many solutions, or no solutions. In the first two case, find the solution(s) as well. cty - 2z = 14 2x + 2y - 4z = 28 6x + 3y + 4z = 1 The system has no solutions. O The solution is * = - 88 z = 1. O There are infinitely many solutions, given by C = - 10 z y = 2 83 4 10 z 2 = Z. O There are infinitely many solutions, given by Z =