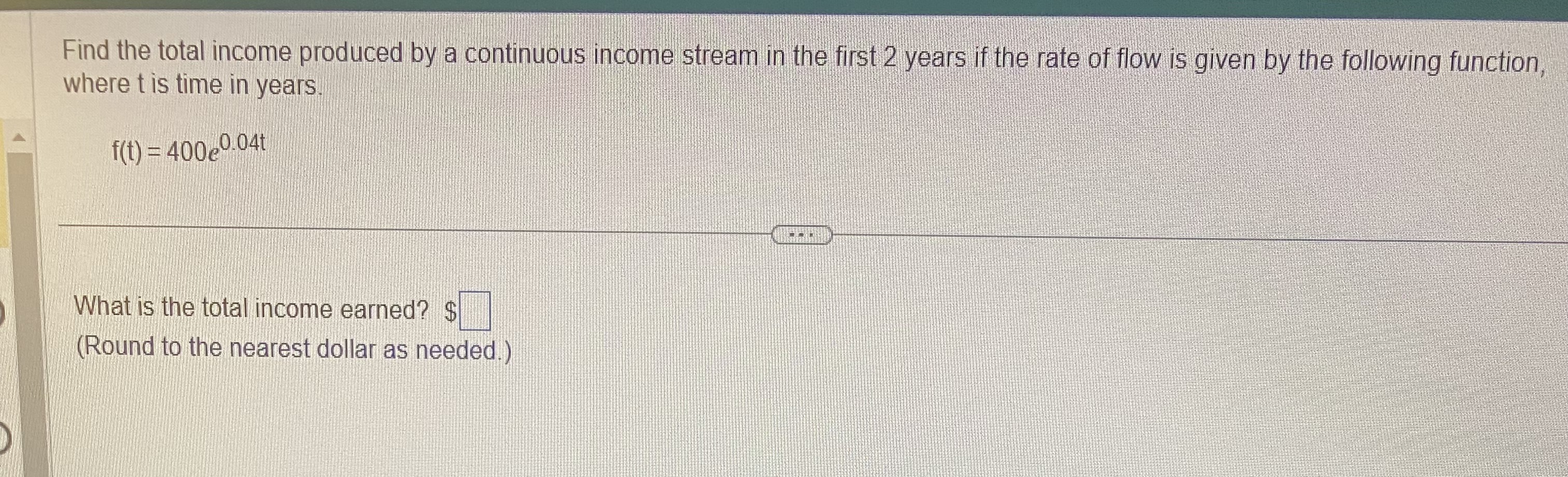
Question: Question 1 Find the total income produced by a continuous income stream in the first 2 years if the rate of flow is given by

Question 1
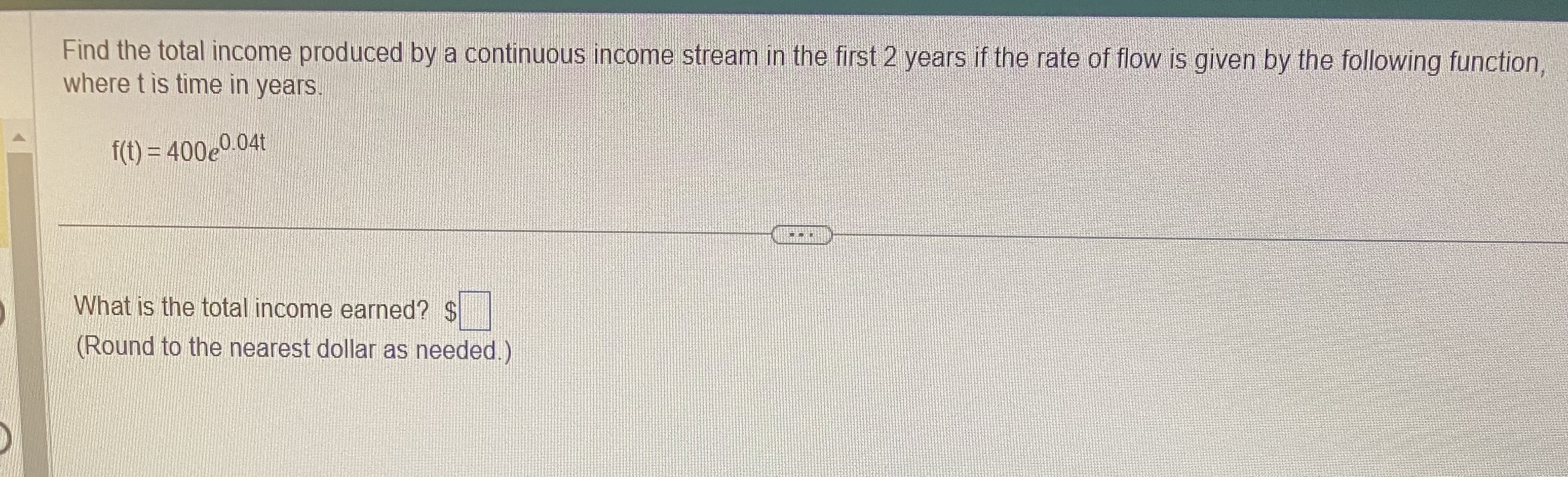


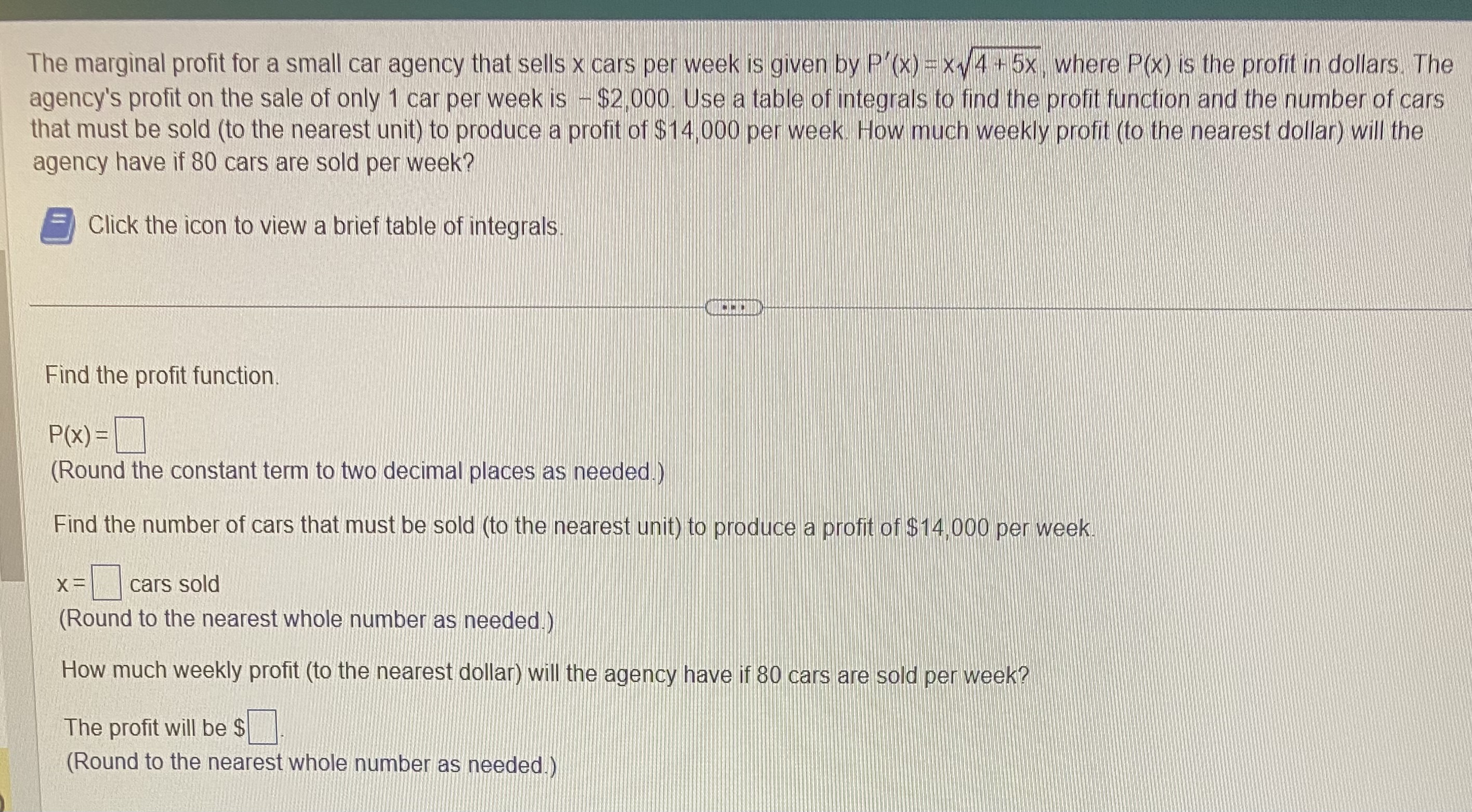
Find the total income produced by a continuous income stream in the first 2 years if the rate of flow is given by the following function, where t is time in years f(t) = 400e0-04t What is the total income earned? $ (Round to the nearest dollar as needed.)The marginal profit for a small car agency that sells x cars per week is given by P'(x) =x /4 + 5x, where P(x) is the profit in dollars. The agency's profit on the sale of only 1 car per week is - $2,000. Use a table of integrals to find the profit function and the number of cars that must be sold (to the nearest unit) to produce a profit of $14,000 per week. How much weekly profit (to the nearest dollar) will the agency have if 80 cars are sold per week? Click the icon to view a brief table of integrals Find the profit function. P(x) = (Round the constant term to two decimal places as needed.) Find the number of cars that must be sold (to the nearest unit) to produce a profit of $14,000 per week X = cars sold (Round to the nearest whole number as needed.) How much weekly profit (to the nearest dollar) will the agency have if 80 cars are sold per week? The profit will be $ (Round to the nearest whole number as needed.)Evaluate the integral 5X xe dx 5X xe dx =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


