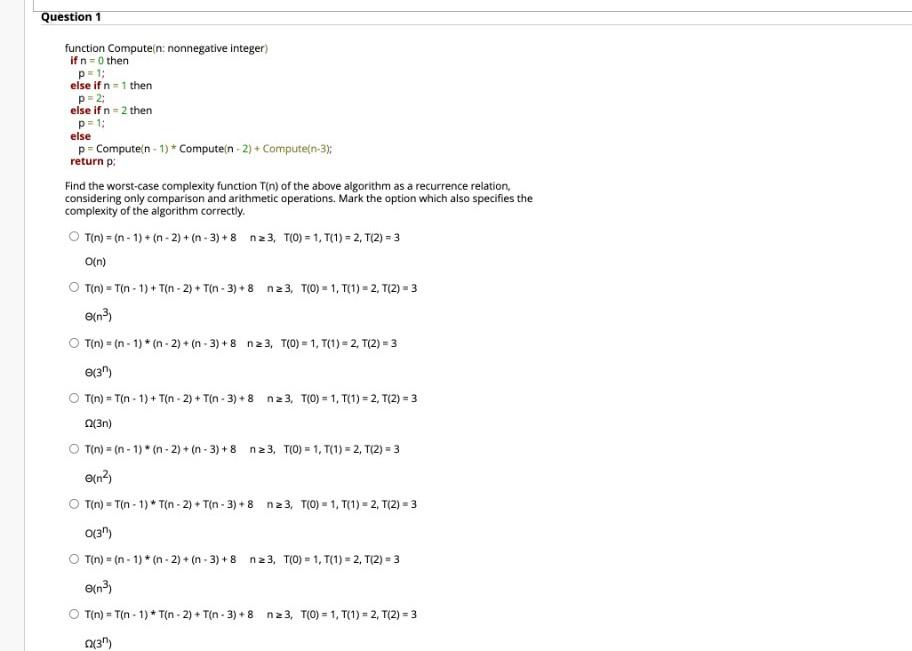
Question 1 function Compute(n: nonnegative Integer) if n=0 then p=1; else if n = 1 then p=2; else ifn - 2 then p=1 else p = Compute(n-1) + Compute(n-2) + Compute(n-3): return p: Find the worst-case complexity function Tin) of the above algorithm as a recurrence relation, considering only comparison and arithmetic operations. Mark the option which also specifies the complexity of the algorithm correctly. Tin) = (n-1) + (n -2) + (n -3)+8 123, TO) = 1, T(1) = 2, T(2) = 3 O(n) T(n) = Tn - 1) + Tn - 2) + Tr - 3) + 8 n23, T(O) = 1, T1) = 2, T2) = 3 e(n) O T(n) = (n - 1) + (n - 2) + (n - 3) + 8 n23, T(0) = 1, T(1) = 2, T(2) = 3 (3") Tn) = (n - 1) + Tn - 2) + Tn - 3) + 8 n23, T(O) = 1, T(1) = 2, T(2) = 3 (3n) T(n) = (n-1)(n-2) + (n-3)+8 n 23, TO) = 1, T(1) = 2, T(2) = 3 (n2) Tin) = T(n-1) T(n -2) +T(n-3)+8 123, TO) = 1, T(1) = 2, T(2) = 3 | 0(3) T(n) = (n - 1)*(n-2) + (n - 3)+8 n23, TO) = 1, T(1) = 2, T(2) = 3 e(n) T(n) = T(n-1) * Tn - 2) +T(n-3) + 8 n23, TO) = 1, T(1) = 2, T(2) = 3 + - 0(3)