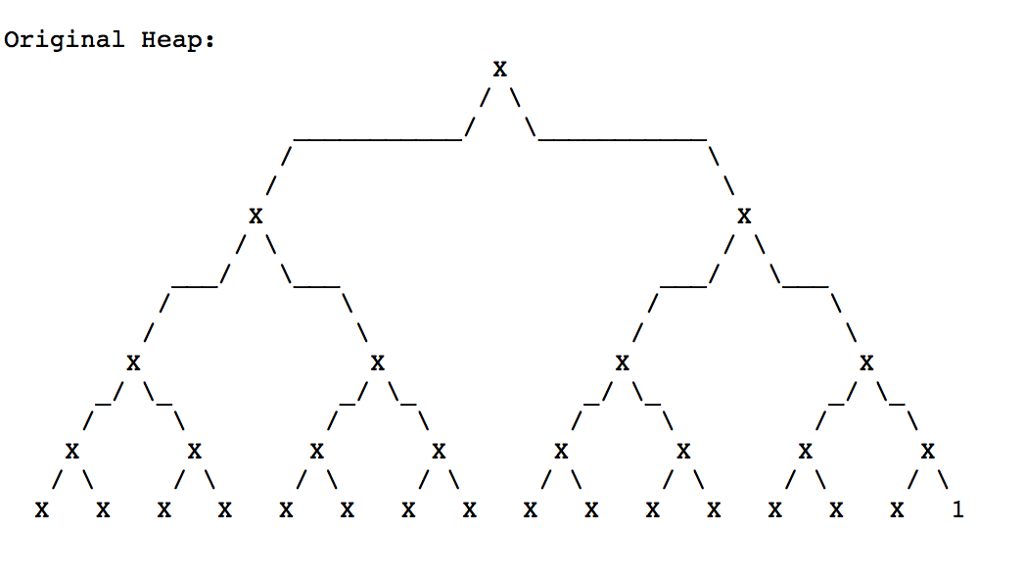
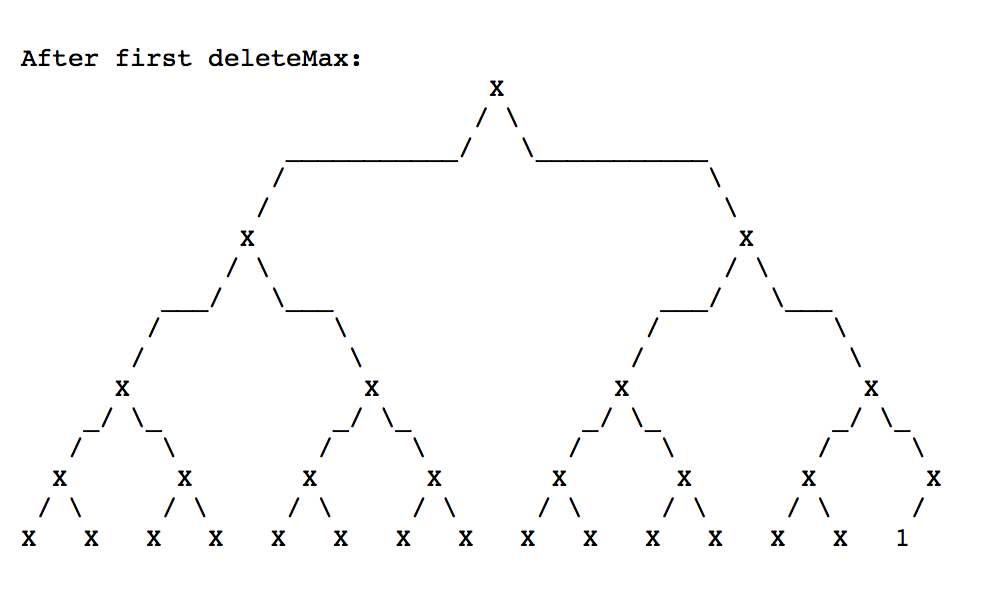
Question: Question 1 In a max heap (largest value at the root), when we call deleteMax, the root is replaced by the last item in the

Question 1 In a max heap (largest value at the root), when we call deleteMax, the root is replaced by the last item in the heap and "trickles down" to the correct position. In the binary heap below, the last item happens to be 1. Replace the X's with actual positive values (no duplicates), so you have a legal max heap and after each of the 4 calls to deleteMax, the number 1 trickles down to the last position again. "Draw" the resulting heap after each deleteMax. (You might want to copy over your original heap four times instead of entering the numbers again.)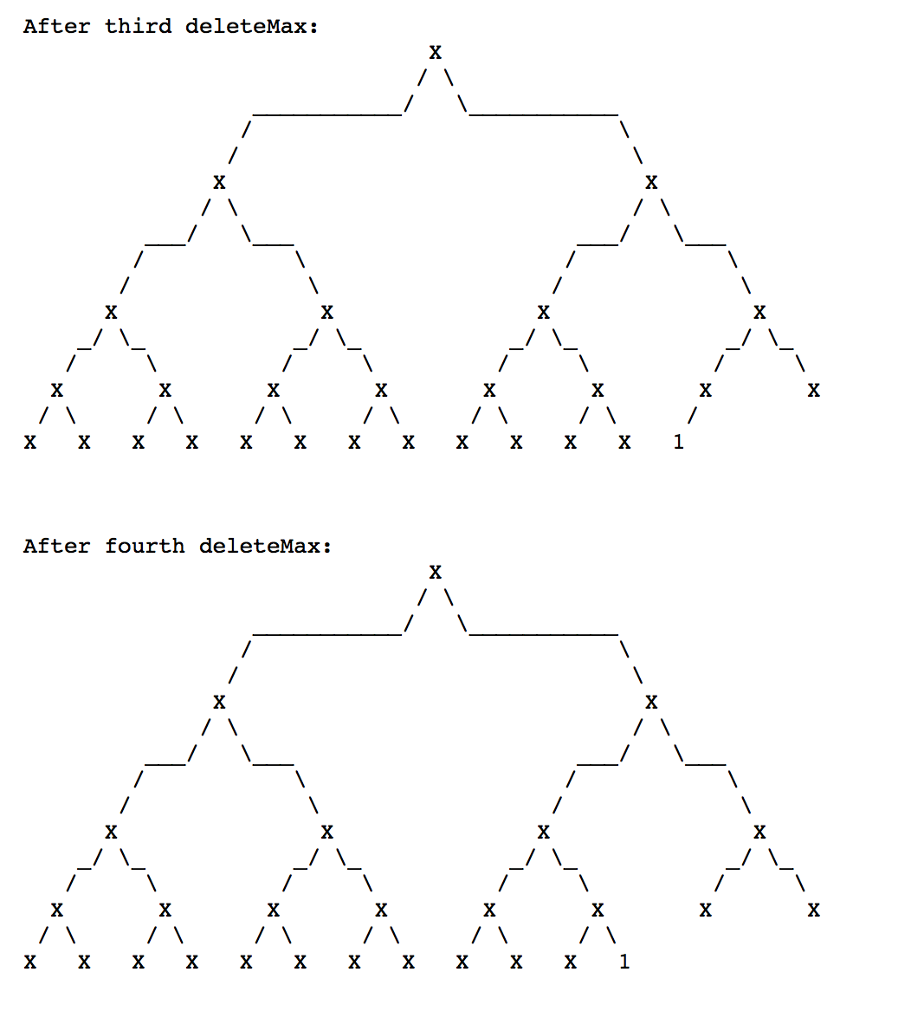

Original Heap

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

dont use tabs In a max heap (largest value at the root), when we call deleteMax, the root is replaced by the last item in the heap and "trickles down" to the correct position. In the binary heap...

Hello I need help I'm stuck and I dont have time . I dont know if you need it but I have posted an Appendix containing ADT specification The class needed for this question and mostly commented...

Hello I need help writing a class. You "might" need other source files too and I have posted them below please. This is the question package lib280.tree; public class IterableArrayedHeap280 > extends...

Python Programming question? plz use template.py below plus some test cases provided def left(i): return 2 * i + 1 # considering 0 indexed array def right(i): return 2 * i + 2 # considering 0 indexed...

TypeError: 'int' object is not callable class MedianMaintainHeap: class MaxHeap: def __init__(self): self.H = [None] self.size = 0 def size(self): return len(self.H)-1 def __repr__(self): return...

Question 3 : Heaps . ( a ) 1 0 points Below are three different methods for building a max - heap. Suppose that A [ 1 , 2 , . . . , n ] initially contains n elements, which are not necessarily in...

I'm working in C++ and the project im'm working on involves a heap. Below is what the assignment have to do. Below that is what code I have already. Where i'm stuck is i don't know how store the...

Question 3 : Heaps . ( a ) Below are three different methods for building a max - heap. Suppose that A [ 1 , 2 , . . . , n ] initially contains n elements, which are not necessarily in heap format....

Implement a Priority Queue ADT with efficient Enqueue and Dequeue operations (and only these two) using a max heap to store queue items. A max heap is a complete binary tree, implemented using an...

P1 Consider a method for a binary search tree that decides whether the tree is height balanced as defined in section 23.10. A tree is said to be height balanced or simply balanced if the subtrees of...

Southwest Airlines (SWA) was one of the most successful airline companies in the 1990s. Throughout the decade, it was the only major domestic airline to turn a profit, and it consistently...

1. Let RA be simple return on asset A, Rg be simple return on asset B and Wo be initial wealth. Assume Riid N(,, o), i = A.B cov (RA, RB) = OAB, Corr(RA, RB) = PAB. where A B and A> OB. Consider the...

In order for investors to purchase stock in a company, they will require a return of at least a certain amount. The amount investors require depends on which of the following? Group of answer choices...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

4. Move around while on a videoconference to improve interpersonal communication; sitting rigid will result in loss of persuasiveness.

3. Realize that trust will be measured almost exclusively in terms of reliability.

How are members held accountable for serving in the assigned roles?