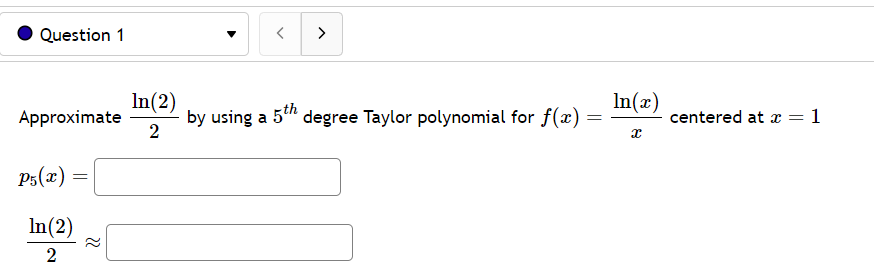
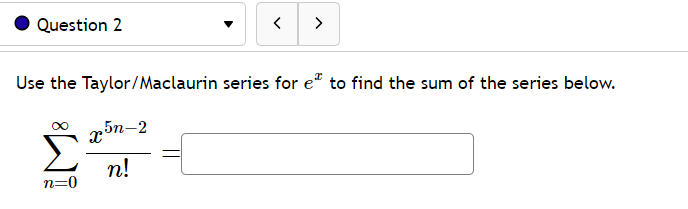
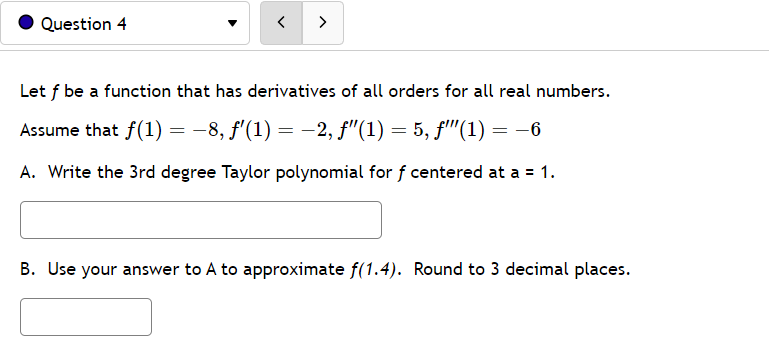
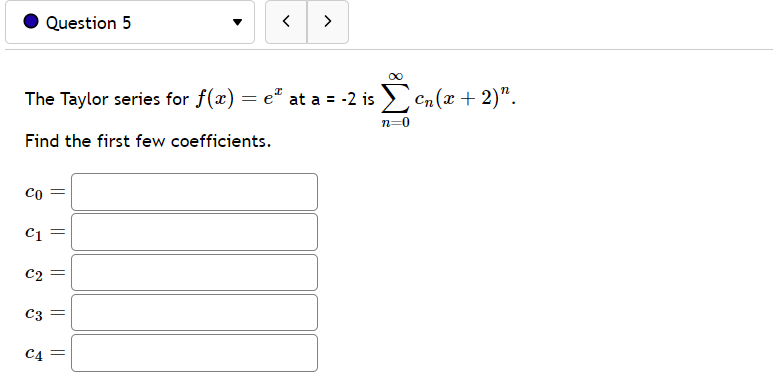
. Question 1 > In(2) In(ac) Approximate centered at x = 1 2 by using a 5th degree Taylor polynomial for f(a) = P5(2) = In(2) 2. Question 2 > Use the Taylor/Maclaurin series for e" to find the sum of the series below. OO 5n-2 n! n=0@ Question 3 v Find the function to which the given series converges within its interval of convergence. Use exact values. ) 24 . L6 8 ) 210 - 3 7 9 5 Question 4 v Let f be a function that has derivatives of all orders for all real numbers. Assume that f(1) = 8, f'(1) = -2, f(1) =5, f"(1) = 6 A. Write the 3rd degree Taylor polynomial for f centered at a = 1. B. Use your answer to A to approximate f(7.4). Round to 3 decimal places. Question 5 > The Taylor series for f(a) = e" at a = -2 is Cn (a + 2 ) ". n=0 Find the first few coefficients. CO C1 C2 = C3 = C4