Question: Question 1: Let F =. Use Stokes' Theorem to evaluate curlF . dS, where S S consists of the top and the four sides (but
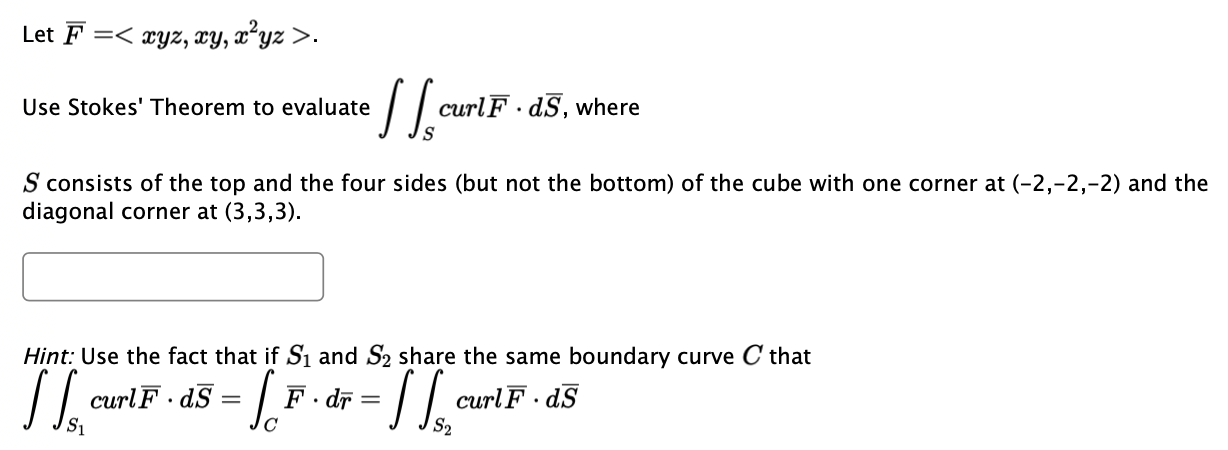


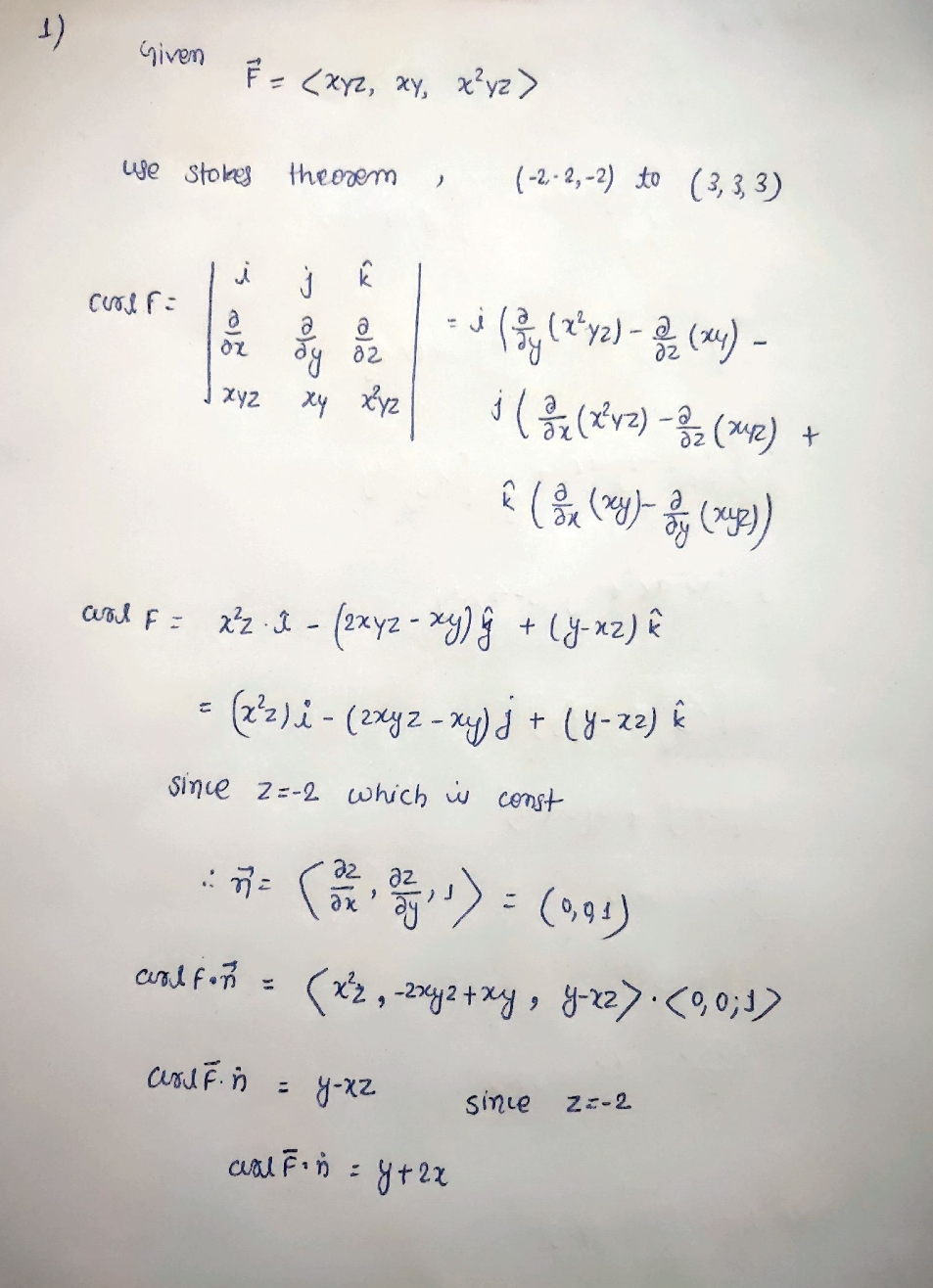
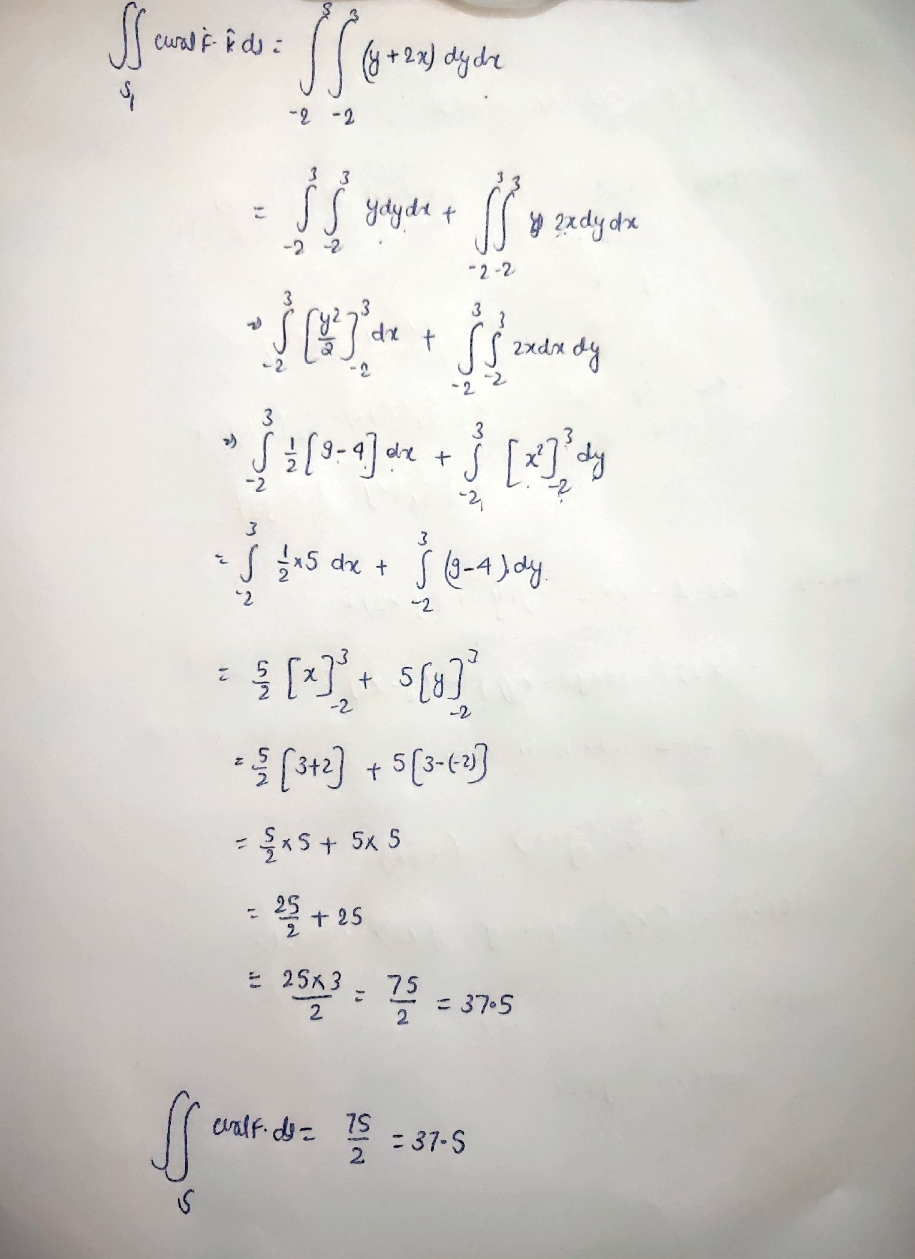

Question 1:
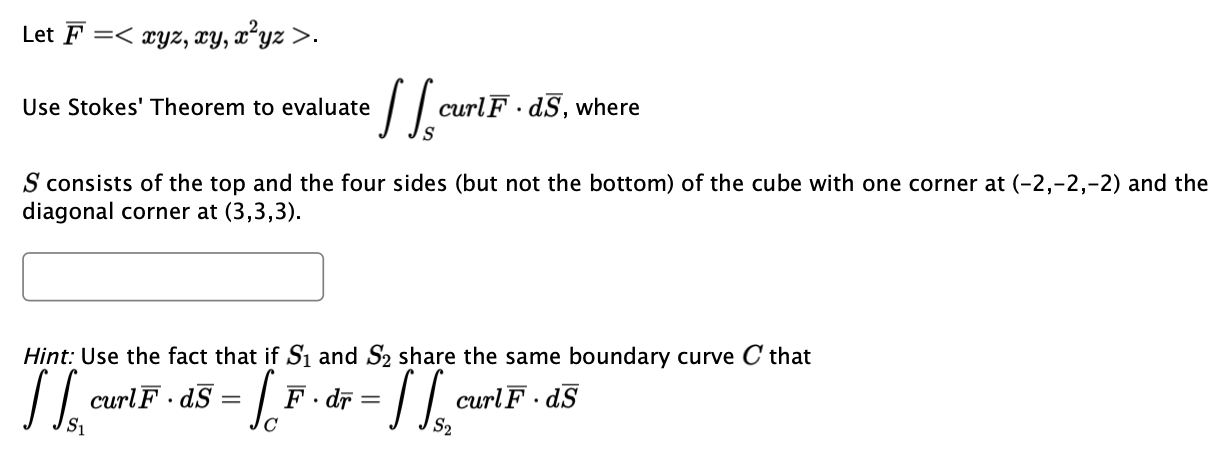


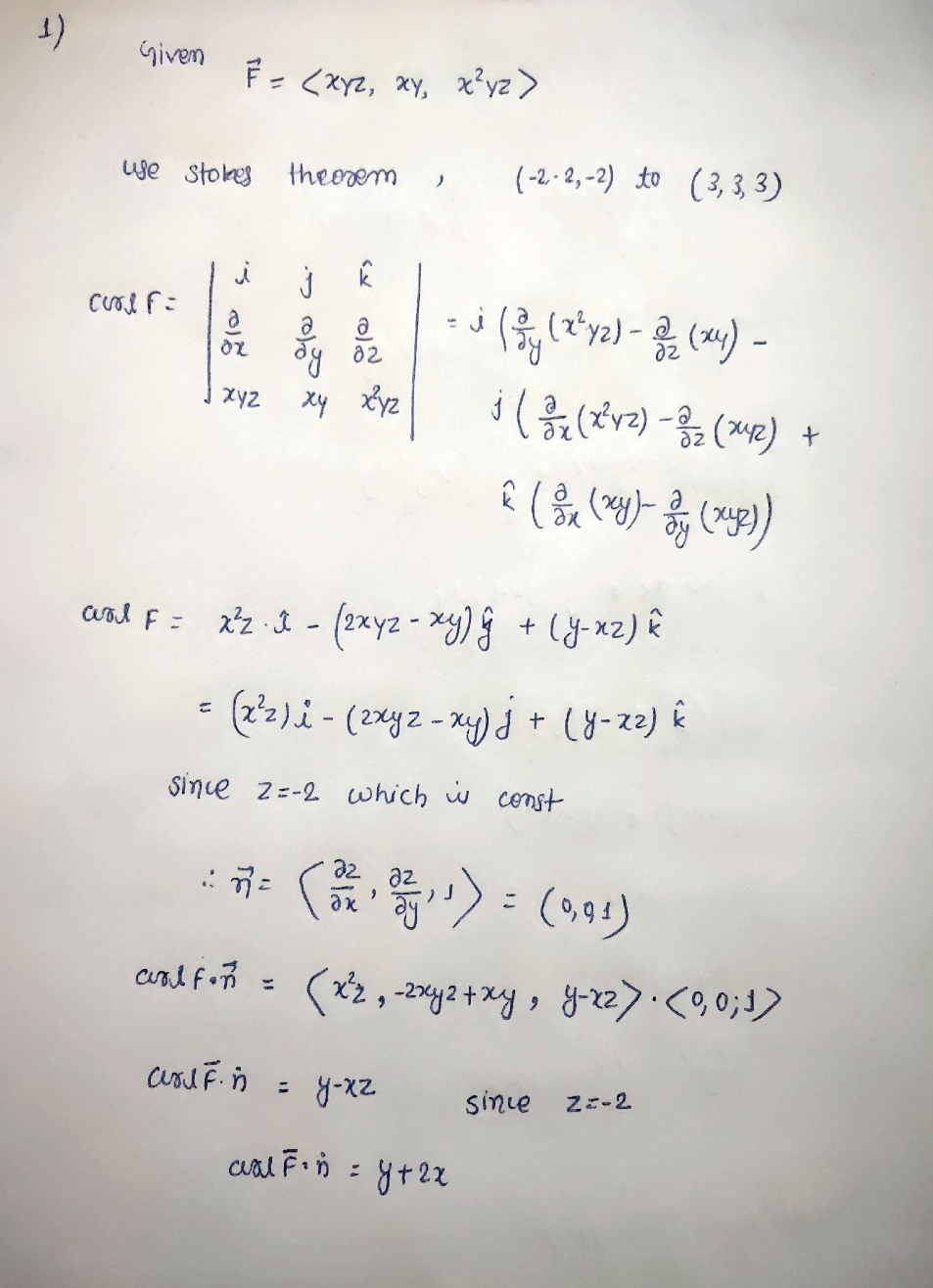
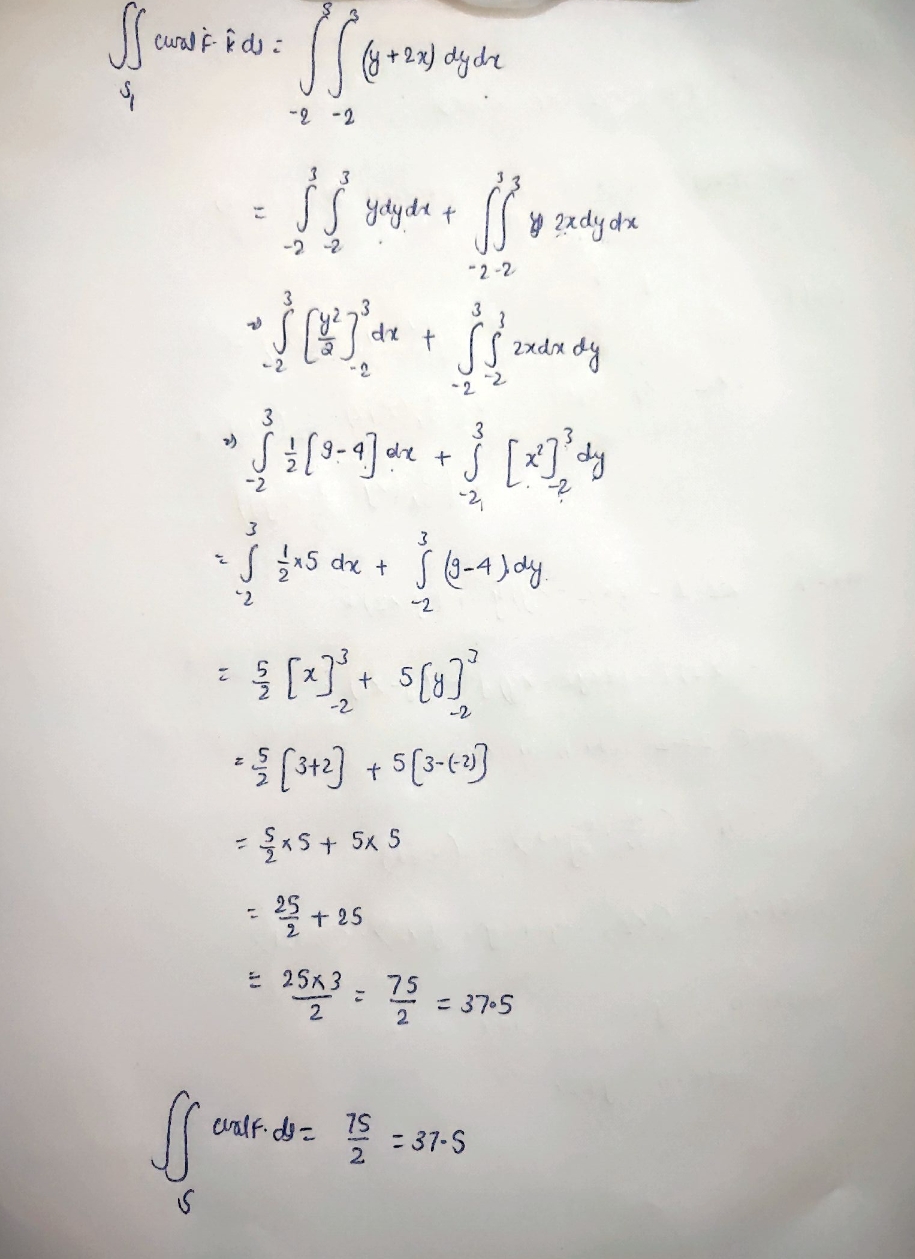

Let F =. Use Stokes' Theorem to evaluate curlF . dS, where S S consists of the top and the four sides (but not the bottom) of the cube with one corner at (-2,-2,-2) and the diagonal corner at (3,3, 3). Hint: Use the fact that if S1 and S2 share the same boundary curve C that curlF . as = F . dr = curlF . dS S2Let F = Use Stokes' Theorem to evaluate F . dr, where C is the triangle with vertices (8,0,0), (0,8,0), and (0,0,8), oriented counterclockwise as viewed from above.2) F = Curd F = k a ( 0 , 0 , 8 ) a x Re az 2 X47 84+22 424 XR x = j (0 - 22 ) - 5 ( 2X - 0 ) + * ( 0-24) = 1(-22 ) + j (-22 ) + 1x (-24) = soface integral can be converted into area integral of walf . do = IS ( GULF ) . NOLA R = SS
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


