Question 1

Let Xt be a zero-mean, unit-variance stationary process with autocorrelation ?k. Suppose that ?t is a non-constant function and that ?t is a positive-valued non-constant function. The observed series is formed as ?Yt=?t+?tXt.?

(i) Find the mean and covariance function for the Yt process

(ii) Is the process Yt stationary?

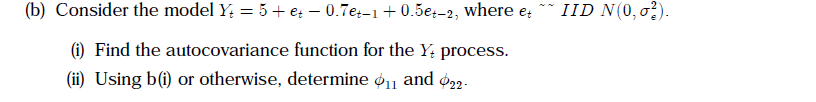
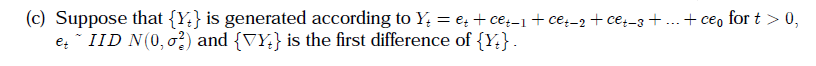
(b) Consider the model Yt = 5 + et - 0.7et-1 + 0.5et-2, where et "IID N(0, o). (i) Find the autocovariance function for the Yt process. (ii) Using b(i) or otherwise, determine $1, and $22-{e} Suppeee that {1:} is generated according to 1:; : at + Get1 + (1634 + (2:314 + + can for t :> I]1 at ' LID N00, 03) and {Vii} is the rst difference of {fig}