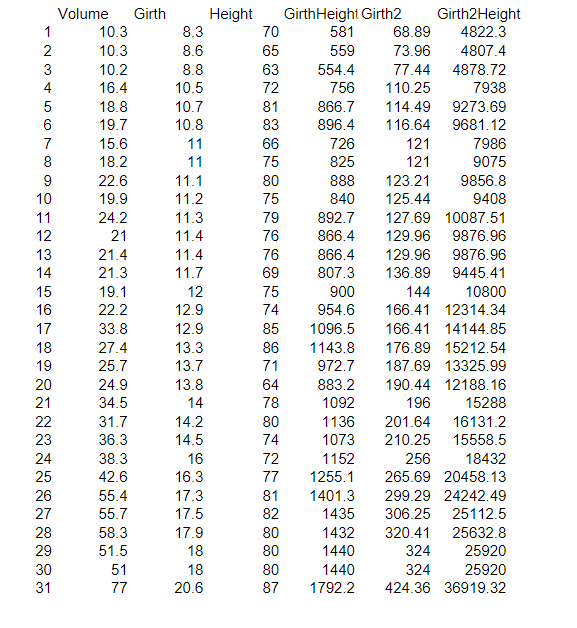
Question: Question 1: Program a function, making use oflm()to fit the linear regression model, that outputs the six coefficient estimates. Set R's seed to 2 :
Question 1:
Program a function, making use oflm()to fit the linear regression model, that outputs the six coefficient estimates.Set R's seed to 2:
set.seed(2, sample.kind = "Rounding")
and then useboot()to produceR= 1000 bootstrap estimates for each of?(0), ?(1),?(2),?(3),?(4), and?(5)
Enter your R code below.
Use your bootstrap estimates to estimate the standard error,SE(?(hat)i), for each ofi= 0, 1, 2, 3, 4, 5.
Question 2:
SE(?(hat)0) =
Question 3:
SE(?(hat)1) =
Question 4:
SE(?(hat)2) =
Question 5:
SE(?(hat)3) =
Question 6:
SE(?(hat)4) =
Question 7:
SE(?(hat)5) =
Question 8:
The standard errors estimated from usual linear regression methods are shown in the R output below:
Coefficients:
Estimate Std.Error t value PR(>|t|)
(Intercept) 48.914179 90.852925 0.538 0.595
Girth -8.228180 13.803580 -0.596 0.556
Height -0.616152 1.250446 -0.493 0.626
GirthHeight 0.103075 0.180291 0.572 0.573
Girth2 0.311160 0.536379 0.580 0.567
Girth2Height -0.001764 0.006621 -0.266 0.792
How do these values compare to the standard errors computed in the previous set of questions?
Choose one of the following:
- The estimates from usual linear regression methods aregreater.
- The estimates from usual linear regression methods areless.
- The two sets of estimates areabout the same.
\f
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


