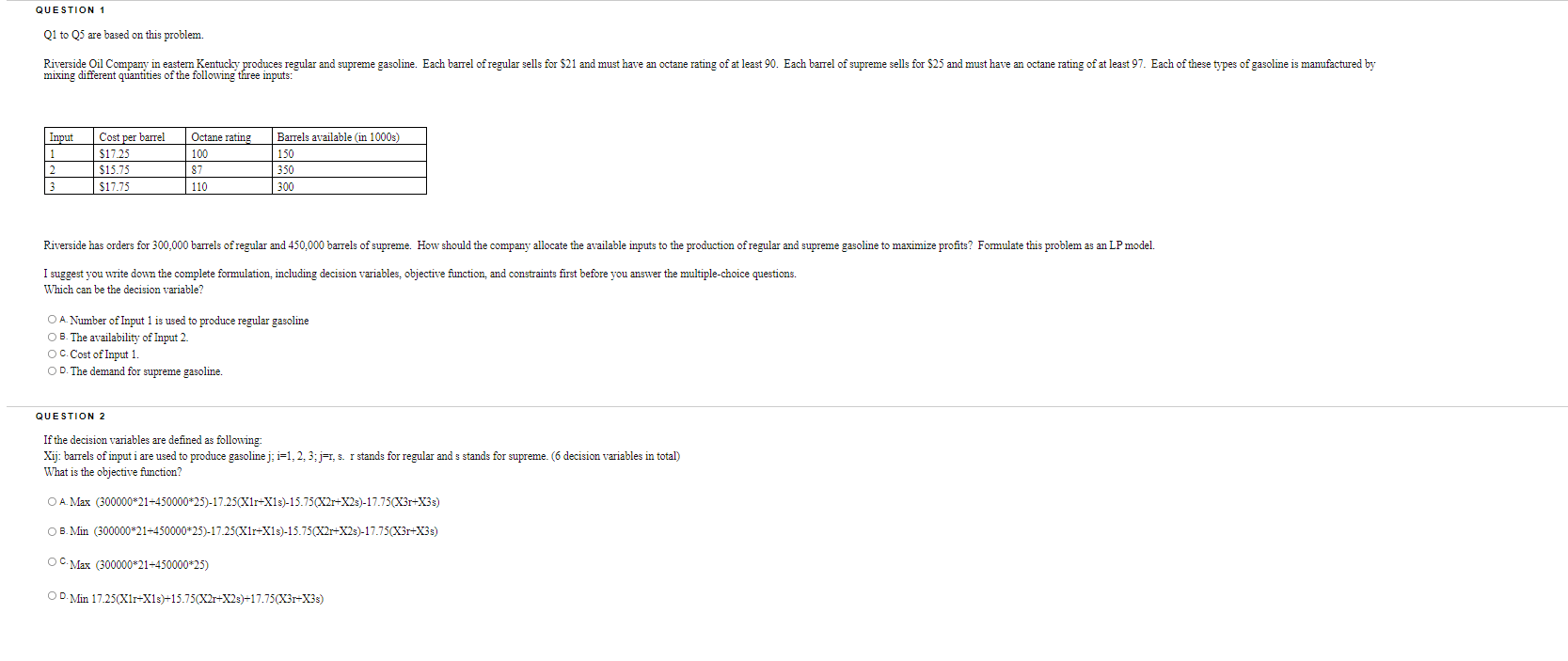
QUESTION 1 Q1 to Q5 are based on this problem. Riverside Oil Company in eastern Kentucky produces regular and supreme gasoline. Each barrel of regular sells for $21 and must have a octane rating of at least 90. Each barrel of supreme sells for $25 and must have an octane rating of at least 97. Each of these types of gasoline is manufactured by mixing different quantities of the following three inputs: Input 1 2 3 Cost per barrel $17.25 $15.75 $17.75 Octane rating 100 87 110 Barrels available in 1000s) 150 350 300 Riverside has orders for 300,000 barrels of regular and 450,000 barrels of supreme. How should the company allocate the available inputs to the production of regular and supreme gasoline to maximize profits? Formulate this problem as an LP model. I suggest you write down the complete formulation, including decision variables, objective function, and constraints first before you answer the multiple-choice questions. Which can be the decision variable? O A. Number of Input 1 is used to produce regular gasoline OB. The availability of Input 2. OC. Cost of Input 1. OD. The demand for supreme gasoline. QUESTION 2 If the decision variables are defined as following: Xij: barrels of input i are used to produce gasoline j; i=1,2,3; j1, 3. r stands for regular and s stands for supreme (6 decision variables in total) What is the objective function? O A. Max (300000*21-450000*25)-17.25(X1r+X13)-15.75(X2r+X23)-17.75(X3r+X3) OB. Min (300000*21-450000*25)-17.25(X1r+X13)-15.75(X2r+X2s)-17.75(X3r+X33) OC. Max (300000*21-450000*25) OD. Min 17.25(Xir-X13)-15.75(X2r+X23)-17.75(X3r-X3s) QUESTION 1 Q1 to Q5 are based on this problem. Riverside Oil Company in eastern Kentucky produces regular and supreme gasoline. Each barrel of regular sells for $21 and must have a octane rating of at least 90. Each barrel of supreme sells for $25 and must have an octane rating of at least 97. Each of these types of gasoline is manufactured by mixing different quantities of the following three inputs: Input 1 2 3 Cost per barrel $17.25 $15.75 $17.75 Octane rating 100 87 110 Barrels available in 1000s) 150 350 300 Riverside has orders for 300,000 barrels of regular and 450,000 barrels of supreme. How should the company allocate the available inputs to the production of regular and supreme gasoline to maximize profits? Formulate this problem as an LP model. I suggest you write down the complete formulation, including decision variables, objective function, and constraints first before you answer the multiple-choice questions. Which can be the decision variable? O A. Number of Input 1 is used to produce regular gasoline OB. The availability of Input 2. OC. Cost of Input 1. OD. The demand for supreme gasoline. QUESTION 2 If the decision variables are defined as following: Xij: barrels of input i are used to produce gasoline j; i=1,2,3; j1, 3. r stands for regular and s stands for supreme (6 decision variables in total) What is the objective function? O A. Max (300000*21-450000*25)-17.25(X1r+X13)-15.75(X2r+X23)-17.75(X3r+X3) OB. Min (300000*21-450000*25)-17.25(X1r+X13)-15.75(X2r+X2s)-17.75(X3r+X33) OC. Max (300000*21-450000*25) OD. Min 17.25(Xir-X13)-15.75(X2r+X23)-17.75(X3r-X3s)