Question: Question #1 Question #2 A retail store must decide how many Mother's Day cards to have in stock for this year's Mother's Day. Cards must
Question #1
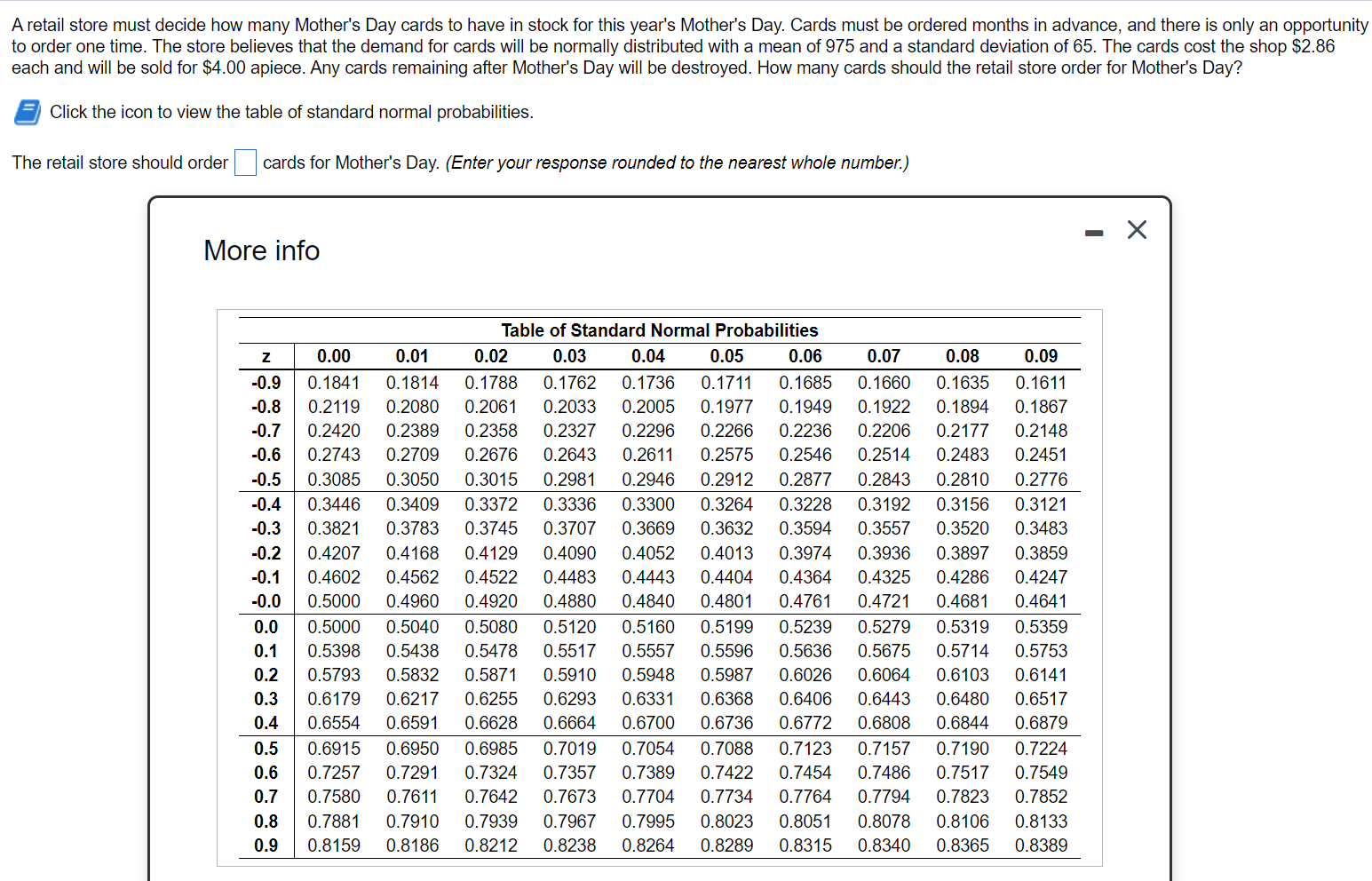
Question #2
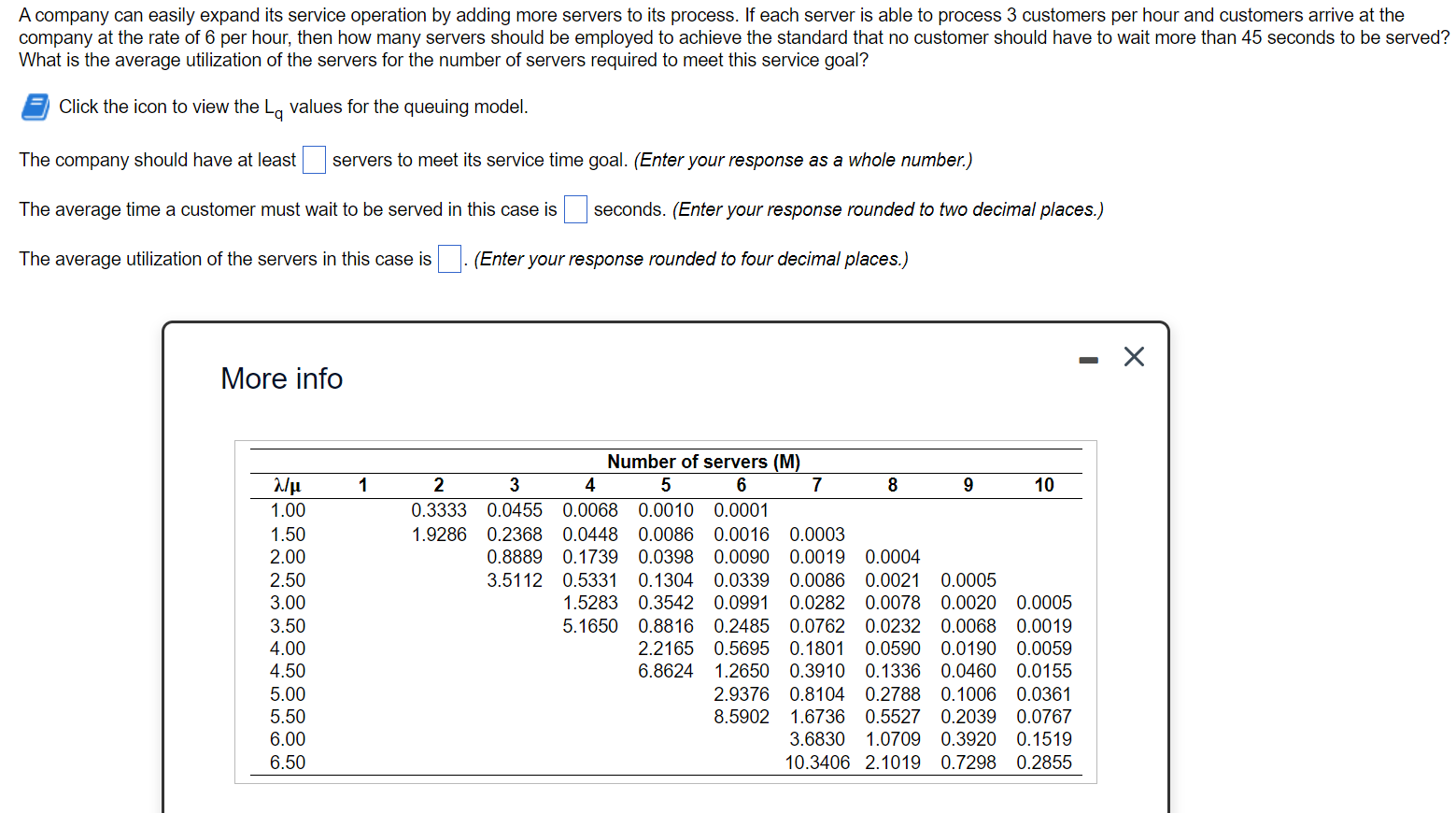
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


