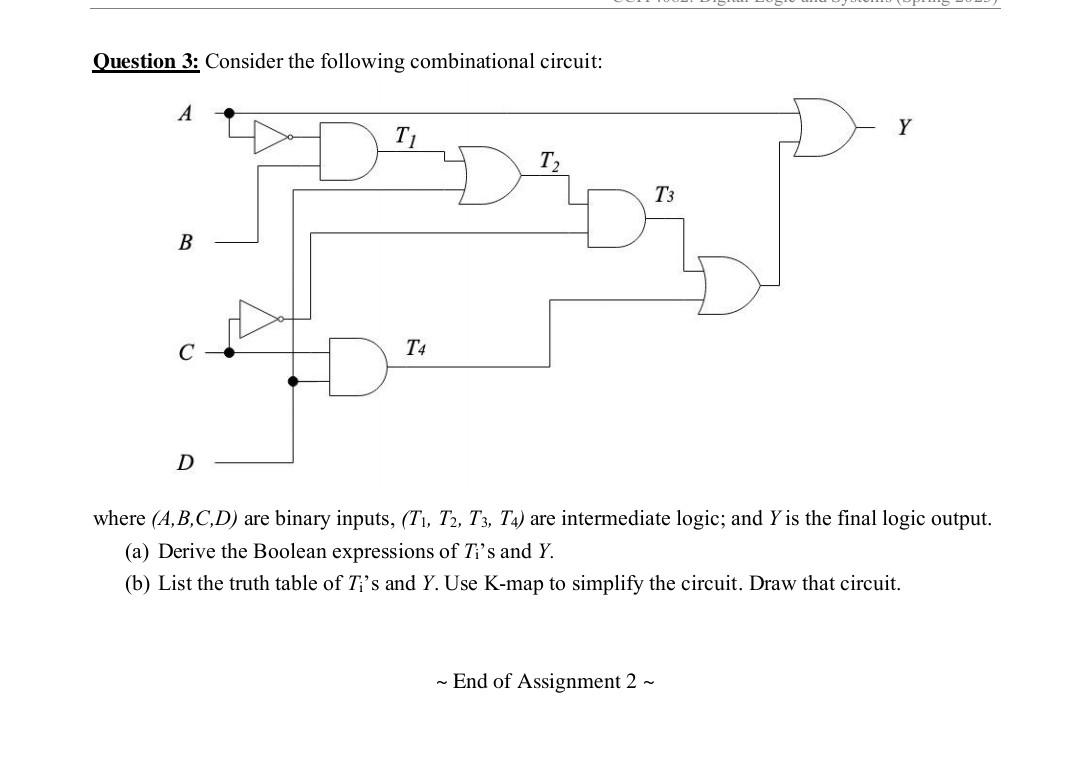
Question 1: Simplify the following Boolean function using the Karnaugh Map. Sketch the circuit diagram for each minimized implementation of the function. (a) F(A,B,C)=m(0,1,2,5) (b) G(w,x,y,z)=m(1,4,5,10) with don't care terms being d(0,7,8,13) Question 2: Consider a Boolean function f(a,b,c,d) (4 binary inputs: a,b,c,d, and 1 output) that outputs the value 1 if and only if the number of 1's in a and b is less than or equal to the number of 1 's in c and d. (a) Write a truth table for function f. (b) Construct K-map for function f, and write the minimal expression for function f in the sum-of-product (SOP) and product-of-sum (POS) forms. Clearly show all the groupings. Question 3: Consider the following combinational circuit: where (A,B,C,D) are binary inputs, (T1,T2,T3,T4) are intermediate logic; and Y is the final logic output. (a) Derive the Boolean expressions of Ti 's and Y. (b) List the truth table of Ti 's and Y. Use K-map to simplify the circuit. Draw that circuit