Question 1. Solve the problem using the MS Excel Solver to find the optimal solution and optimal objective function value. (assume and are continuous decision variables.)

Question 2. Identify binding and non-binding constraints. For each non-binding constraint, what is the value of the slack (or surplus)?

Submission requirement: Note: do NOT specify the decision variables as integer in the Solver.

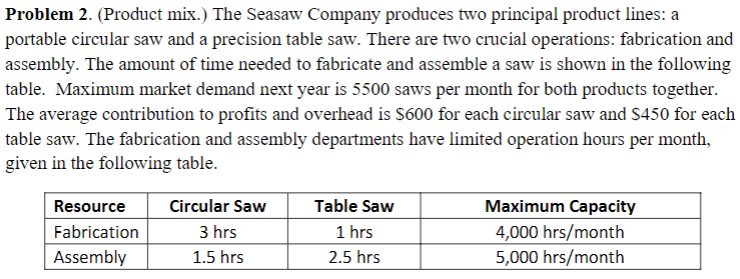
Problem 2. (Product mix.) The Seasaw Company produces two principal product lines: a portable circular saw and a precision table saw. There are two crucial operations: fabrication and assembly. The amount of time needed to fabricate and assemble a saw is shown in the following table. Maximum market demand next year is 5500 saws per month for both products together. The average contribution to profits and overhead is $600 for each circular saw and $450 for each table saw. The fabrication and assembly departments have limited operation hours per month, given in the following table. Problem 2. Recall the "Product mix" in Homework \#1. The problem's formulation is provided as follows: Decision Variables: C is the number of Circular Saws to be produced; T is the number of Table Saws to be produced maxs.t.600C+450T3C+1T40001.5C+2.5T5000C+T5500C0,andT0 (fabrication time) (assembly time) (demand)