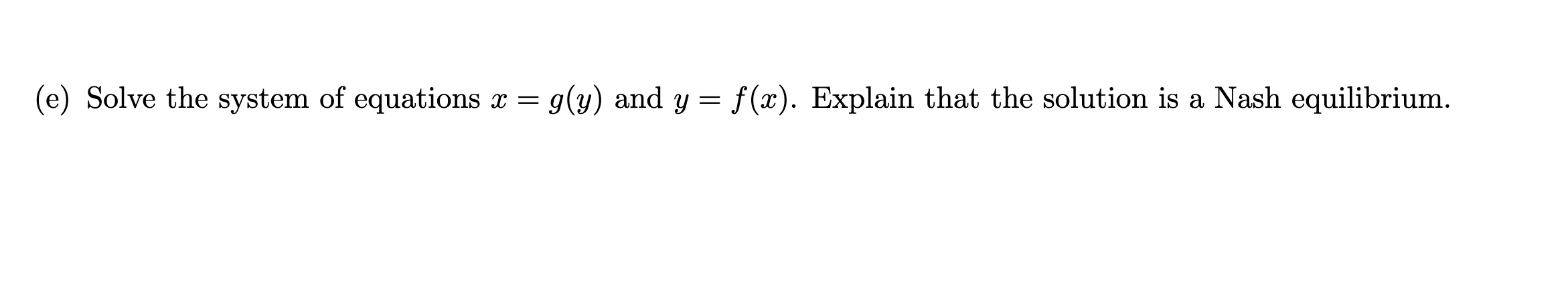
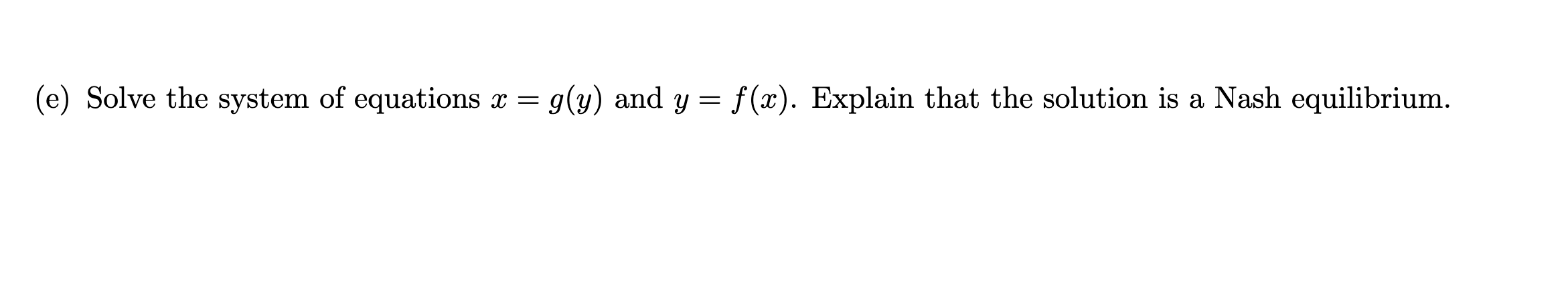
Question 1 . Suppose that two oligopolists A and B produce as and 3; units of a commodity respectively. It is given that : o The price of the commodity is P(ac, y) = 80 025(3) + y). o The cost function for rm A is 01(29) 2 4x -I 100. o The cost function for rm B is 02(y) 2 3y + 125. o The revenue of rm A is P(m, y) - ac. o The revenue of rm B is P(x, 3;) - y. o The prot of a rm is given by its revenue minus its cost. (a) Write down the prot (functions) for A and B in terms of a: and y. \f(b) To find the best response function of A, we regard y as a constant and view the profit of A as a polynomial in x of degree 2. By completing the square, find max that maximizes the profit. Here max, which depends on y, is the best response function of A. In the sequel, we will denote it as g(y).(d) Suppose that A produces x1 = 80 units. Find the best response of B which is denoted by y1. Then find the best response of A for y1 which is denoted by x2 and the best response of B for x2. Repeat this process and obtain X1, X2, 23 ... and y1, y2, y3 .... Do the sequences x1, X2, 23 ... and y1, y2, y3 ... converge?(e) Solve the system of equations x = g(y) and y = f (ac) Explain that the solution is a Nash equilibrium