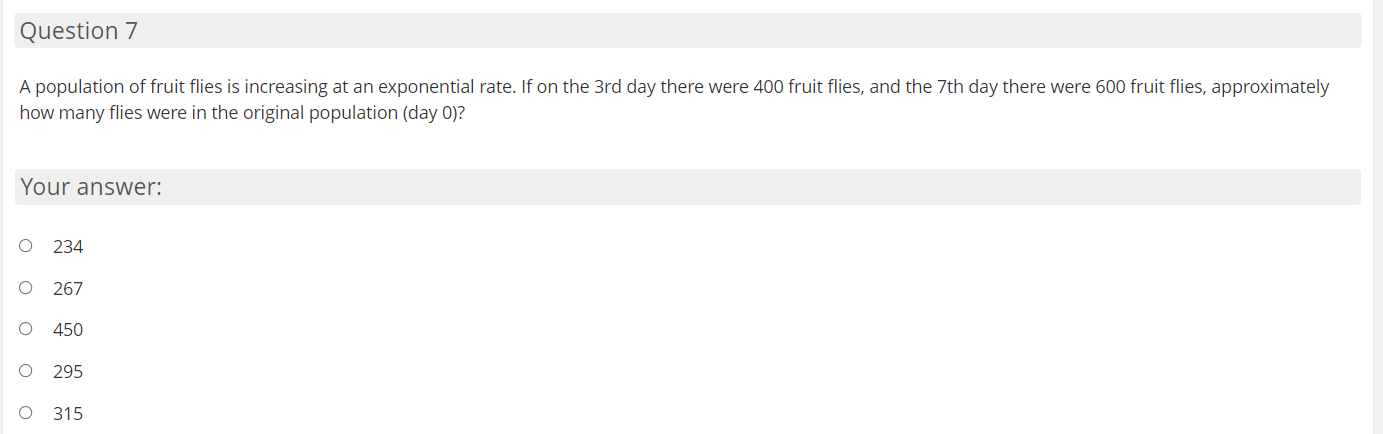
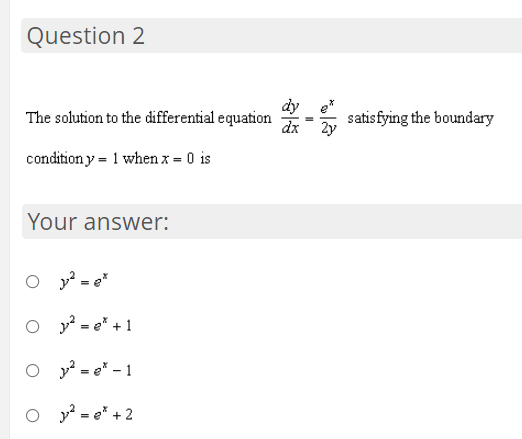
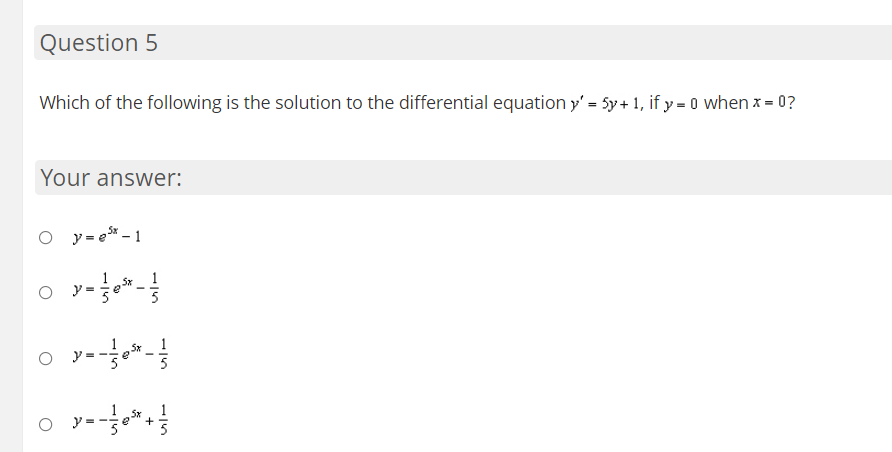
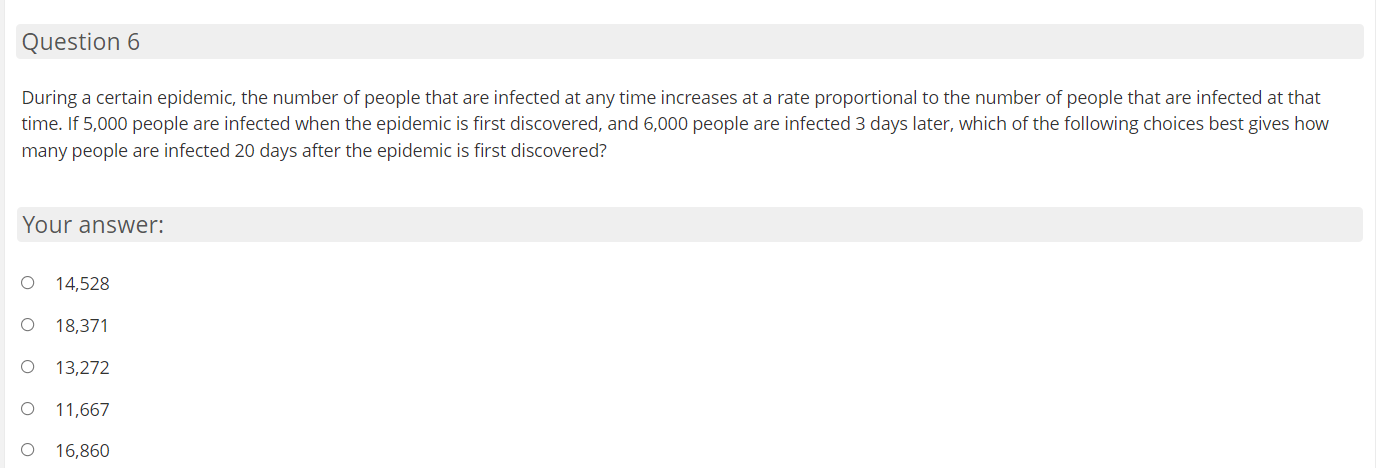
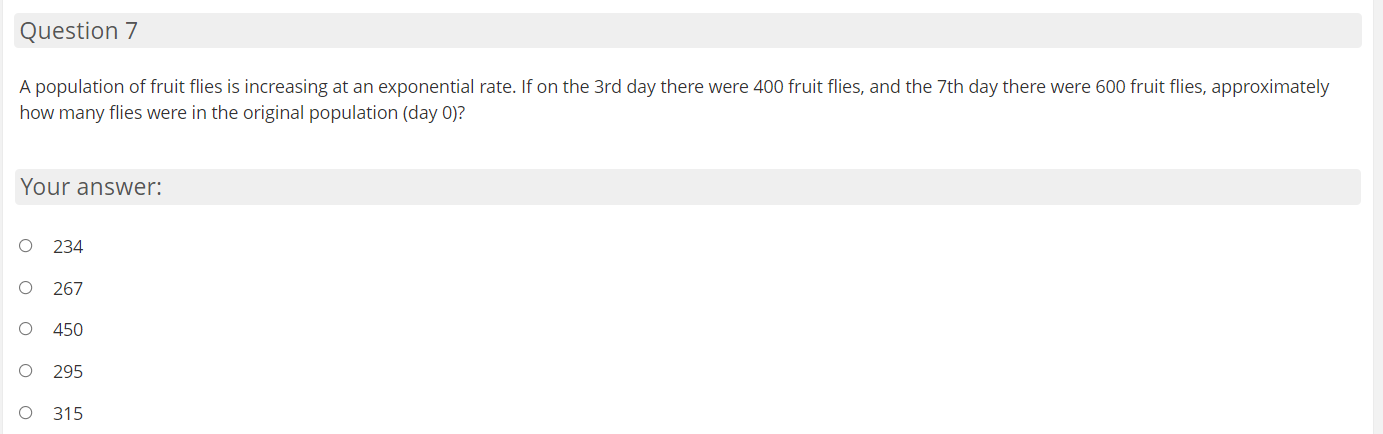
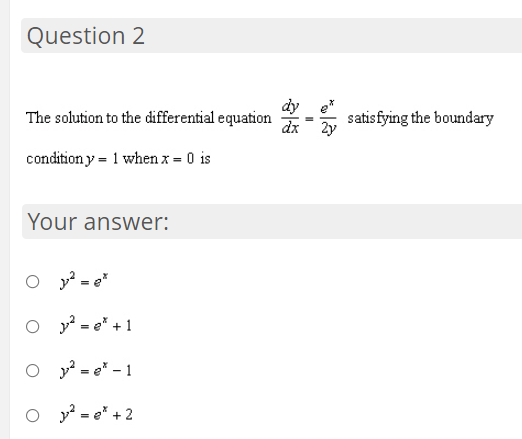
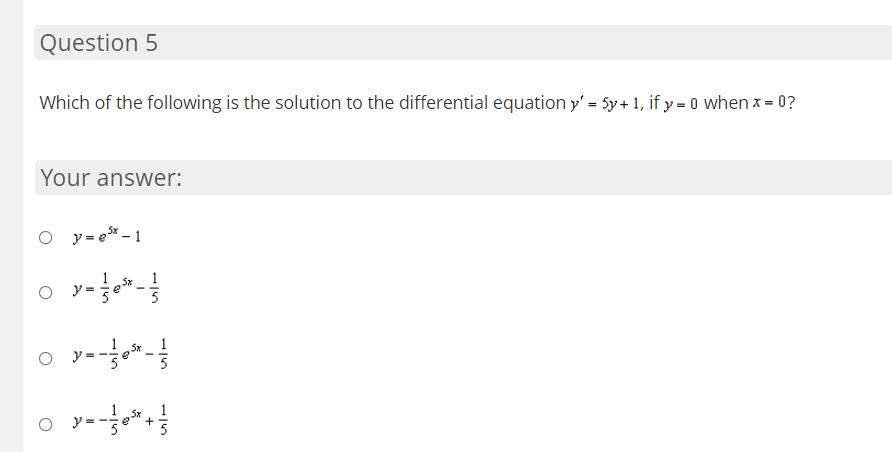
Question 1 The solution to the differential equation dy dx satisfying the boundary condition y = 1 when x = 1 is Your answer: O Y=X O y= x-1 O y=eQuestion 2 The solution to the differential equation dy 2" dx satisfying the boundary condition y = 1 when x = 0 is Your answer: O O +1 O -2 1 O "+ 2Question 3 db: What is the general solution to the differential equation E = 53:9"? Your answer: O y: 51n|5x+ C1 Question 4 What is the general solution to the differential equation dy dx = ()+ 1)(x'+ 1)? Your answer: O y = Co - 1 O y = Ce + 1 O y = Ce - 1 O + X Y = Ce + 1Question 5 Which of the following is the solution to the differential equation y\" = 5y+1. ify- I] when x - I]? Your answer: 0 y-ah-l Question 6 During a certain epidemic. the number of people that are infected at any time increases at a rate proportional to the number of people that are infected at that time. If 5,000 people are infected when the epidemic is first discovered, and 6,000 people are infected 3 days later, which of the following choices best gives how many people are infected 20 days after the epidemic is rst discovered? Your answer: 14.528 18.371 13,272 1 1.667 00000 1 6.860 Question 7 A population of fruit flies is increasing at an exponential rate. If on the 3rd day there were 400 fruit flies, and the 7th day there were 600 fruit flies, approximately how many flies were in the original population {day 0)? Your answer: 234 267 450 295 00000 315