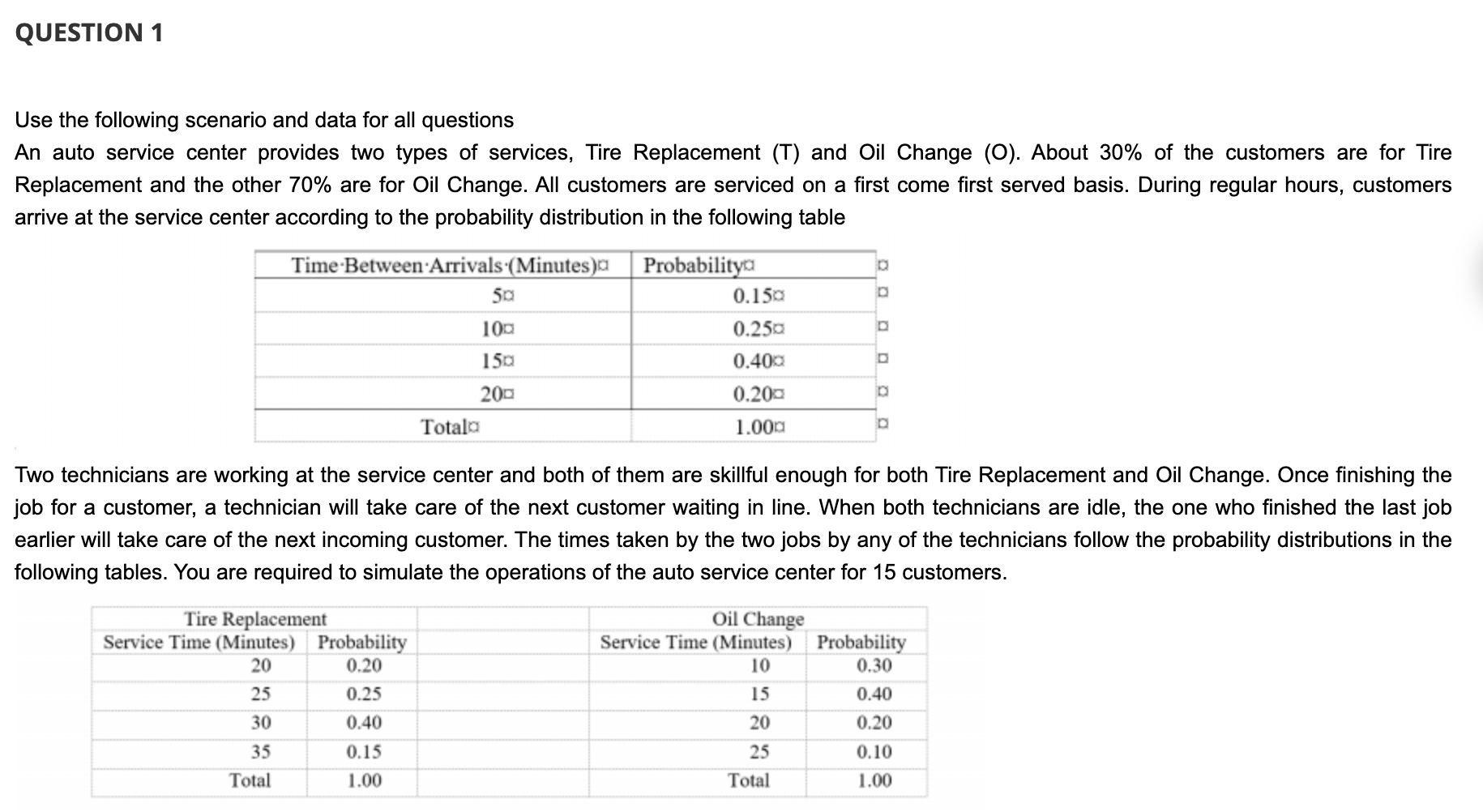
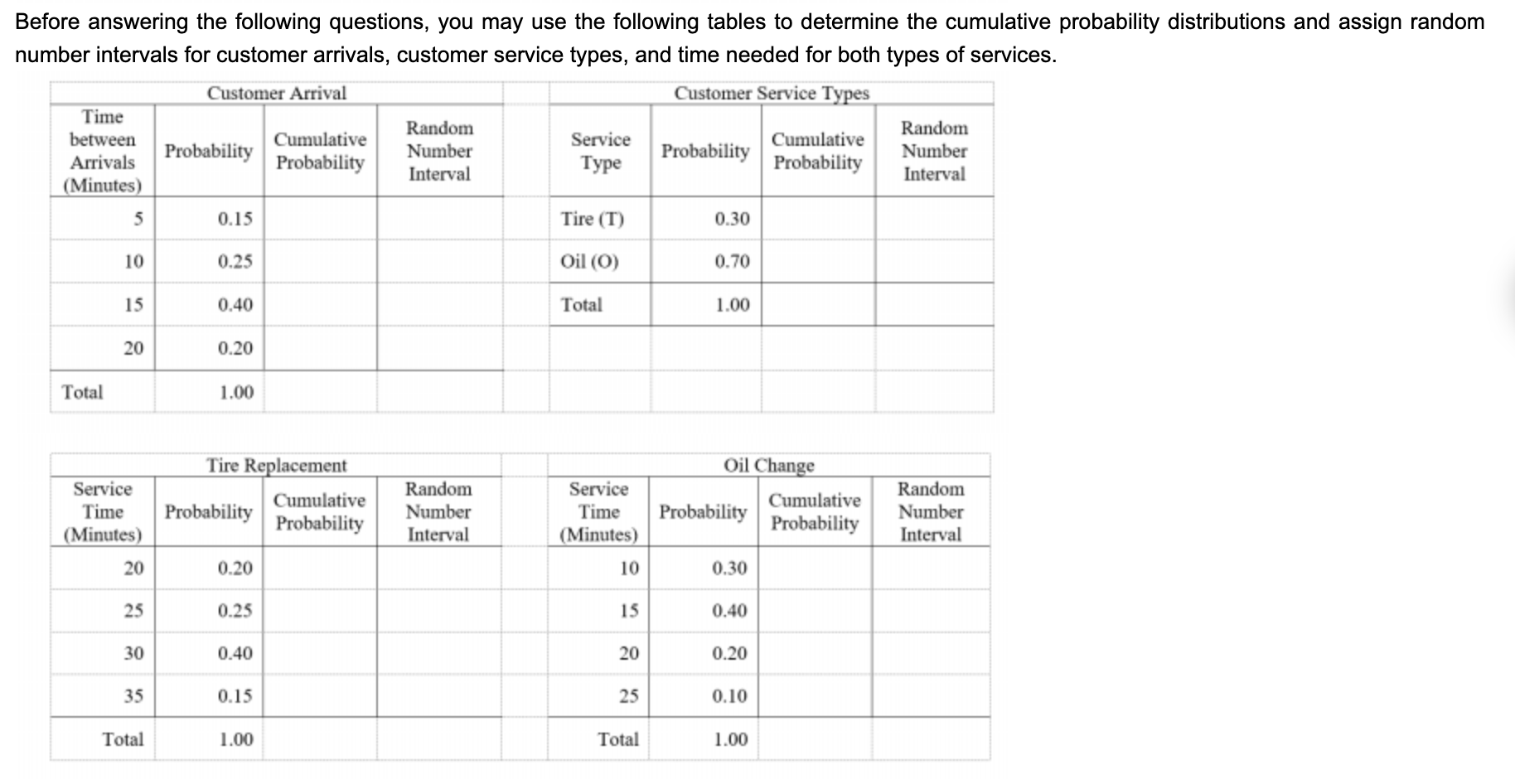
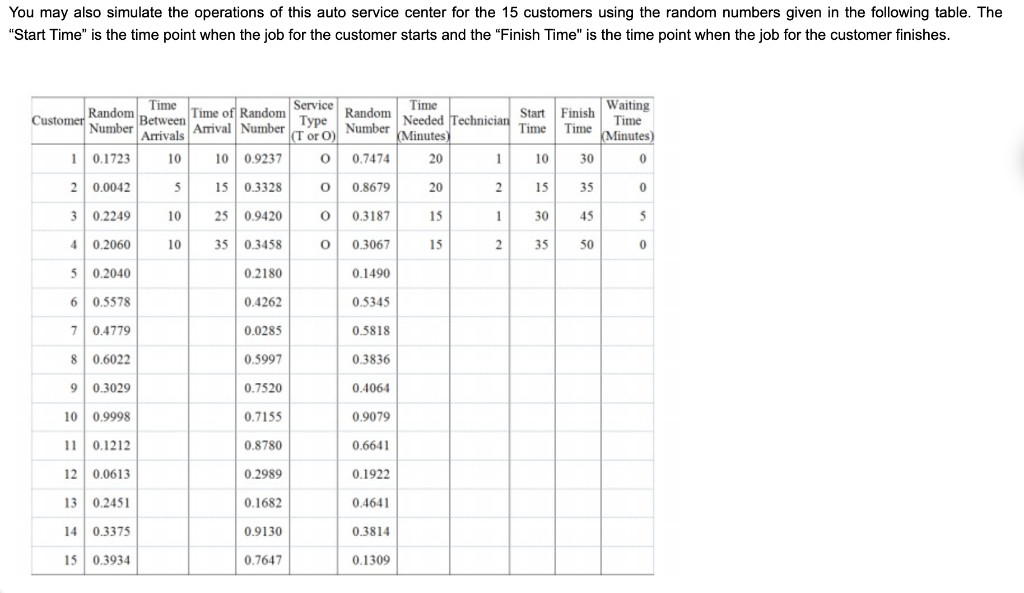
Question: QUESTION 1 Use the following scenario and data for all questions An auto service center provides two types of services, Tire Replacement (T) and Oil

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


