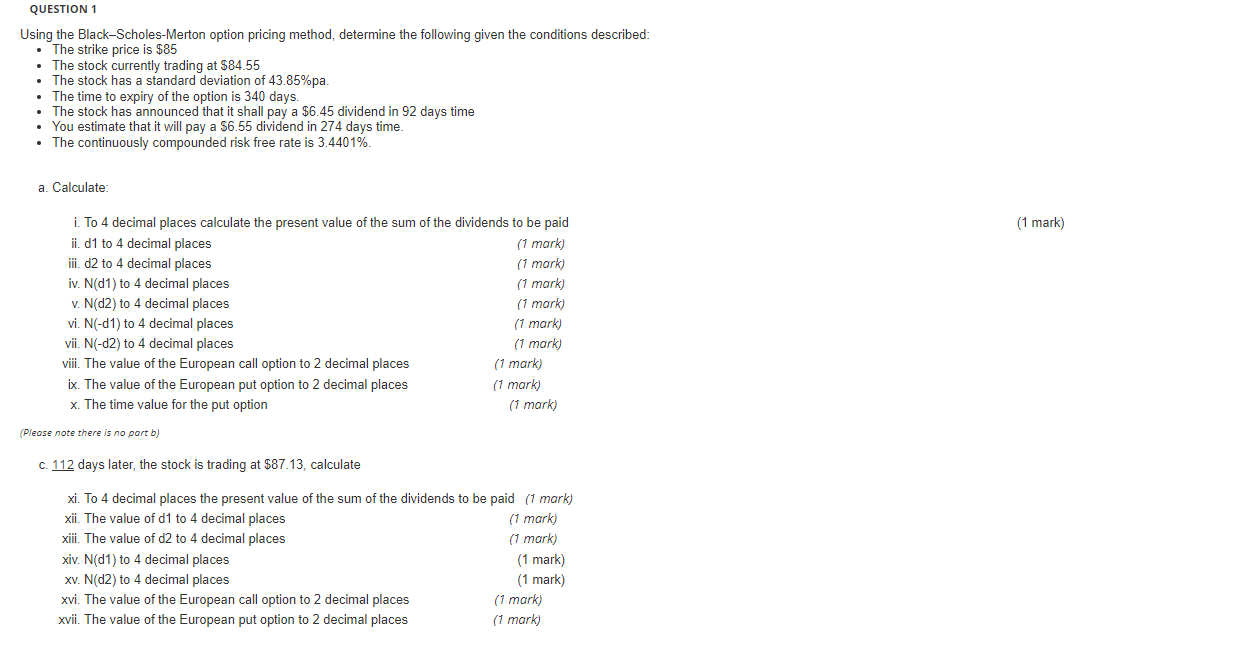
QUESTION 1 Using the Black-Scholes-Merton option pricing method, determine the following given the conditions described: The strike price is $85 . The stock currently trading at $84.55 The stock has a standard deviation of 43.85%pa. The time to expiry of the option is 340 days. The stock has announced that it shall pay a $6.45 dividend in 92 days time You estimate that it will pay a $6.55 dividend in 274 days time. The continuously compounded risk free rate is 3.4401%. a. Calculate: i. To 4 decimal places calculate the present value of the sum of the dividends to be paid ii. d1 to 4 decimal places (1 mark) iii. d2 to 4 decimal places (1 mark) iv. N(d1) to 4 decimal places (1 mark) v. N(d2) to 4 decimal places (1 mark) vi. N(-d1) to 4 decimal places (1 mark) vii. N(-d2) to 4 decimal places (1 mark) viii. The value of the European call option to 2 decimal places ix. The value of the European put option to 2 decimal places x. The time value for the put option (1 mark) (Please note there is no part b) c. 112 days later, the stock is trading at $87.13, calculate xi. To 4 decimal places the present value of the sum of the dividends to be paid (1 mark) xii. The value of d1 to 4 decimal places (1 mark) xiii. The value of d2 to 4 decimal places (1 mark) xiv. N(d1) to 4 decimal places xv. N(d2) to 4 decimal places xvi. The value of the European call option to 2 decimal places xvii. The value of the European put option to 2 decimal places (1 mark) (1 mark) (1 mark) (1 mark) (1 mark) (1 mark) (1 mark) QUESTION 1 Using the Black-Scholes-Merton option pricing method, determine the following given the conditions described: The strike price is $85 . The stock currently trading at $84.55 The stock has a standard deviation of 43.85%pa. The time to expiry of the option is 340 days. The stock has announced that it shall pay a $6.45 dividend in 92 days time You estimate that it will pay a $6.55 dividend in 274 days time. The continuously compounded risk free rate is 3.4401%. a. Calculate: i. To 4 decimal places calculate the present value of the sum of the dividends to be paid ii. d1 to 4 decimal places (1 mark) iii. d2 to 4 decimal places (1 mark) iv. N(d1) to 4 decimal places (1 mark) v. N(d2) to 4 decimal places (1 mark) vi. N(-d1) to 4 decimal places (1 mark) vii. N(-d2) to 4 decimal places (1 mark) viii. The value of the European call option to 2 decimal places ix. The value of the European put option to 2 decimal places x. The time value for the put option (1 mark) (Please note there is no part b) c. 112 days later, the stock is trading at $87.13, calculate xi. To 4 decimal places the present value of the sum of the dividends to be paid (1 mark) xii. The value of d1 to 4 decimal places (1 mark) xiii. The value of d2 to 4 decimal places (1 mark) xiv. N(d1) to 4 decimal places xv. N(d2) to 4 decimal places xvi. The value of the European call option to 2 decimal places xvii. The value of the European put option to 2 decimal places (1 mark) (1 mark) (1 mark) (1 mark) (1 mark) (1 mark) (1 mark)