Question 1:

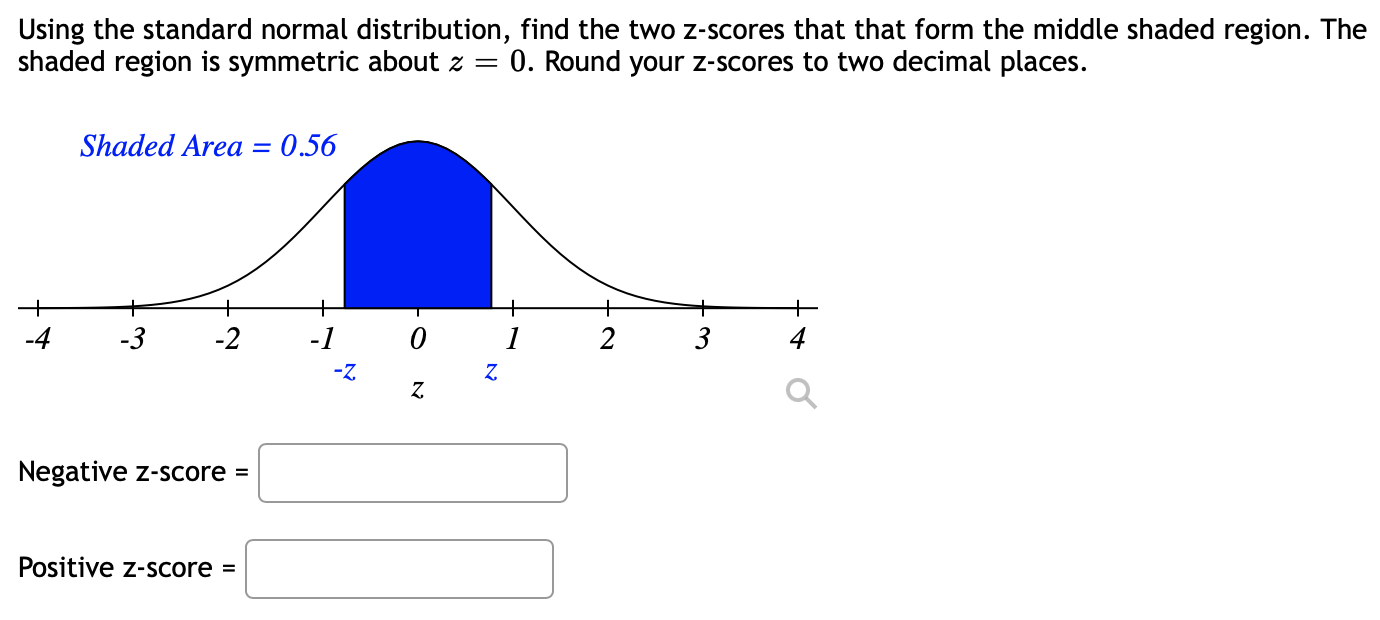
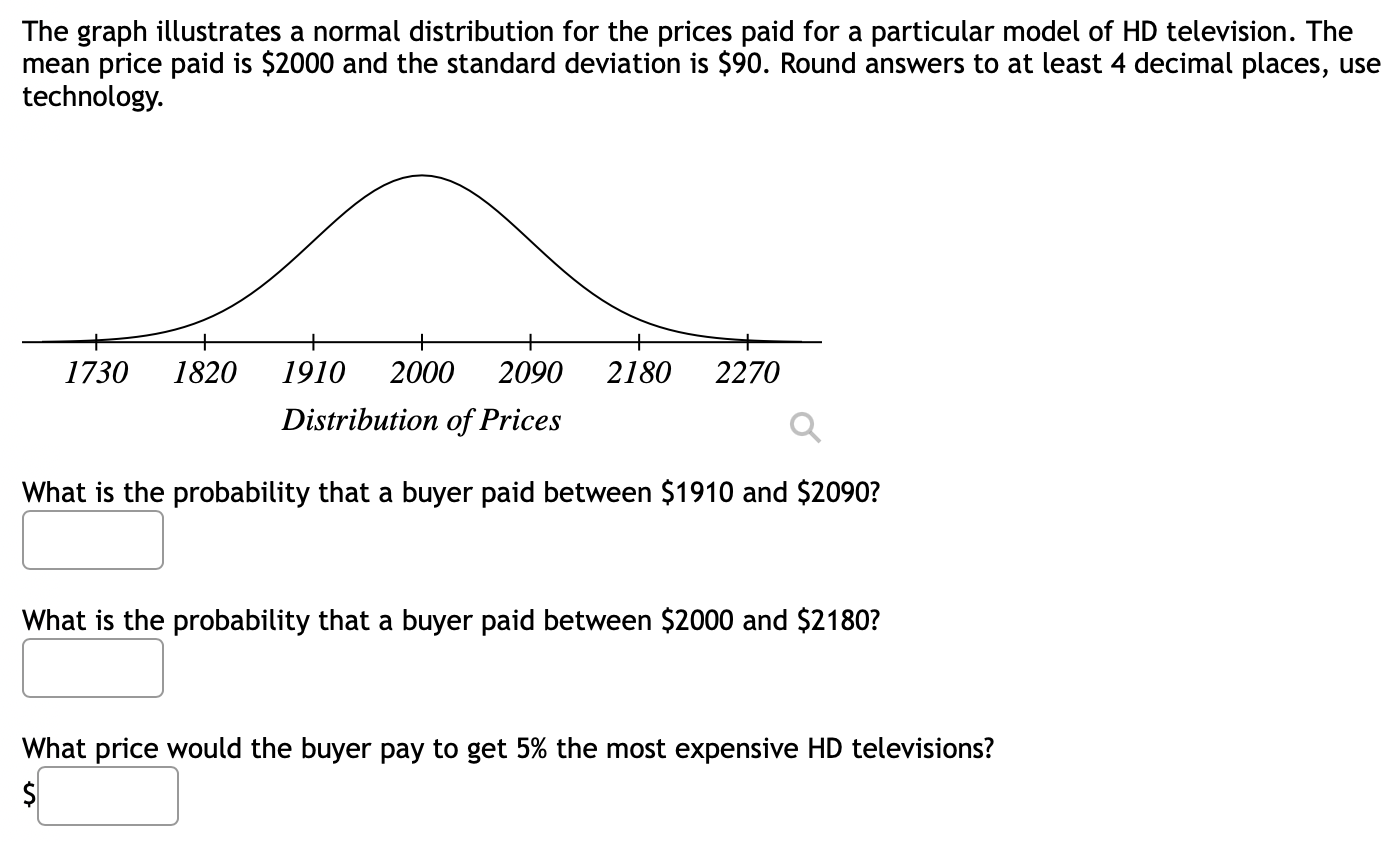
Using the standard normal distribution, find the two z-scores that that form the middle shaded region. The shaded region is symmetric about 2 = 0. Round your z-scores to two decimal places. Shaded Area = 0.56 A normal distribution has a mean of 77 and a standard deviation of 7. Use the standard normal table to find the indicated probability for a randomly selected x-value from the distribution. Round all probabilities to 5 decimal places. Find the z score for 58 P(x 3 58) = Find the z score for 76 P(x 3 76) = P(58 S a: S 76) = A particular fruit's weights are normally distributed, with a mean of 413 grams and a standard deviation of 36 grams. If you pick one fruit at random, what is the probability that it will weigh between 456 grams and 526 grams In the country of United States of Heightlandia, the height measurements of ten-year-old children are approximately normally distributed with a mean of 55.4 inches, and standard deviation of 4.2 inches. A) What is the probability that a randomly chosen child has a height of less than 49.2 inches? Answer- (Round your answer to 3 decimal places.) B) What is the probability that a randomly chosen child has a height of more than 64.5 inches? Answer- (Round your answer to 3 decimal places.) The graph illustrates a normal distribution for the prices paid for a particular model of HD television. The mean price paid is $2000 and the standard deviation is $90. Round answers to at least 4 decimal places, use technology. I 730 1820 1910 2000 2090 2180 22 70 Distribution of Prices (1 What is the probability that a buyer paid between $1910 and $2090? D What is the probability that a buyer paid between $2000 and $2180? D What price would the buyer pay to get 5% the most expensive HD televisions? 5:]