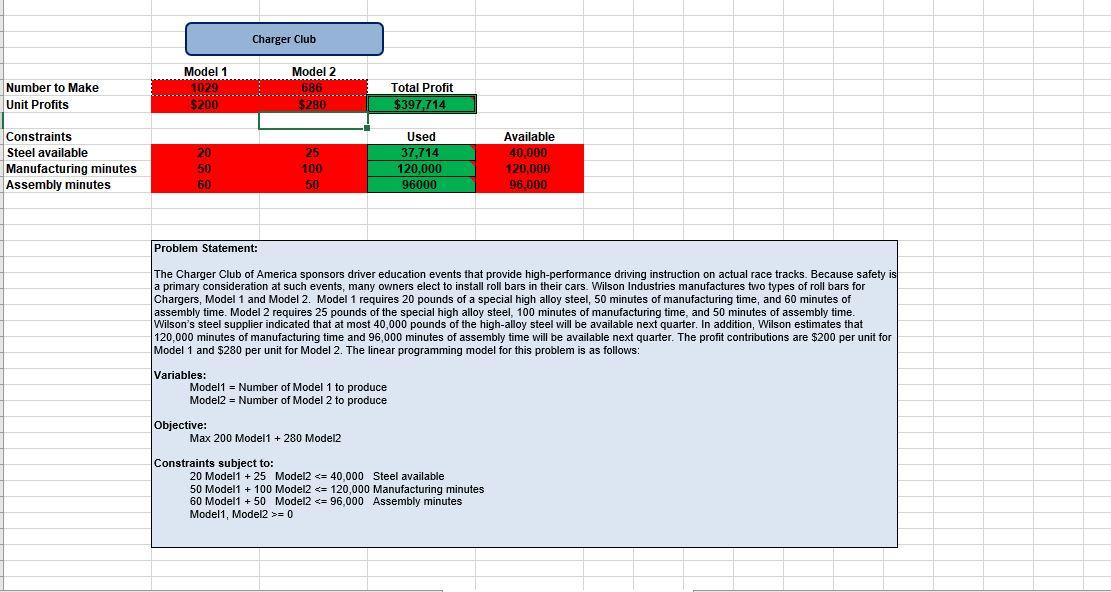
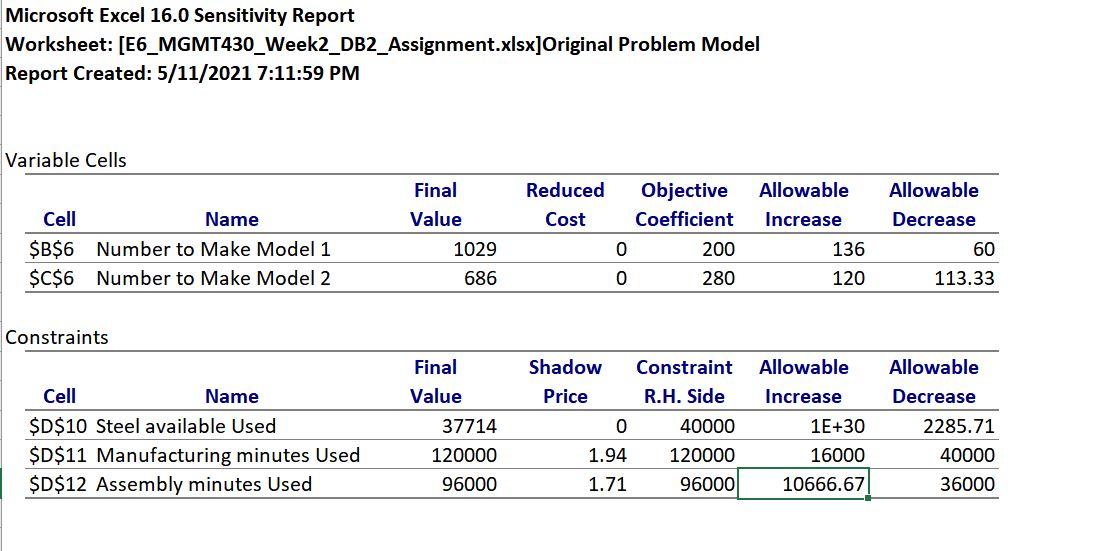
Question 1) What are the optimal solution and the total profit?

Question 2) If the unit profit of the Model 2 decreases to $250 per unit, how would the optimal solution change?

Question 3): How much should the company be willing to pay to acquire additional capacity in the 'Assembly minutes' area? Explain in detail.

Question 4) How much should the company be willing to pay to acquire additional 'Steel'? Explain in detail.

Question 5) How much will the objective function, 'Total Profit', change if there was one additional hour of Manufacturing capacity available?

Charger Club Model 2 Model 1 0:29 Number to Make Unit Profits Total Profit $397 714 300 $280 $200 Constraints Steel available Manufacturing minutes Assembly minutes 20 50 60 25 100 50 Used 37.714 120,000 96000 Available 40,000 120,000 96.000 Problem Statement: The Charger Club of America sponsors driver education events that provide high-performance driving instruction on actual race tracks. Because safety is a primary consideration at such events, many owners elect to install roll bars in their cars. Wilson Industries manufactures two types of roll bars for Chargers, Model 1 and Model 2. Model 1 requires 20 pounds of a special high alloy steel, 50 minutes of manufacturing time, and 60 minutes of assembly time. Model 2 requires 25 pounds of the special high alloy steel, 100 minutes of manufacturing time, and 50 minutes of assembly time. Wilson's steel supplier indicated that at most 40,000 pounds of the high-alloy steel will be available next quarter. In addition, Wilson estimates that 120,000 minutes of manufacturing time and 96,000 minutes of assembly time will be available next quarter. The profit contributions are $200 per unit for Model 1 and $280 per unit for Model 2. The linear programming model for this problem is as follows: Variables: Model1 = Number of Model 1 to produce Model2 = Number of Model 2 to produce Objective: Max 200 Model1 + 280 Model2 Constraints subject to: 20 Model1 + 25 Model2 =0 Microsoft Excel 16.0 Sensitivity Report Worksheet: [E6_MGMT430_Week2_DB2_Assignment.xlsx]Original Problem Model Report Created: 5/11/2021 7:11:59 PM Variable Cells Reduced Final Value 1029 Allowable Decrease Cell Name $B$6 Number to Make Model 1 $C$6 Number to Make Model 2 Cost Allowable Increase 136 Objective Coefficient 0 200 0 280 60 686 120 113.33 Constraints Cell Name $D$10 Steel available Used $D$11 Manufacturing minutes Used $D$12 Assembly minutes Used Final Value 37714 120000 96000 Shadow Constraint Price R.H. Side 0 40000 1.94 120000 1.71 96000 Allowable Increase 1E+30 16000 10666.67 Allowable Decrease 2285.71 40000 36000