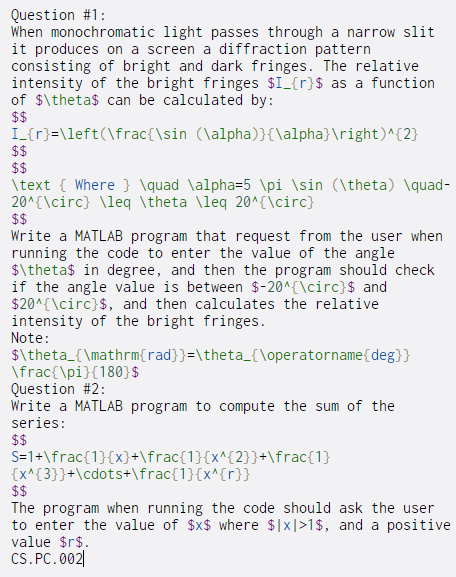
$$ Question #1: When monochromatic light passes through a narrow slit it produces on a screen a diffraction pattern consisting of bright and dark fringes. The relative intensity of the bright fringes $I_{r}$ as a function of $\theta$ can be calculated by: I_{r}=\left(\frac{ \sin (\alpha)}{\alpha} ight)^{2} $$ $$ \text { Where } \quad \alpha=5 \pi \sin (\theta) \quad- 20^{\circ} \leq \theta \leq 20^{\circ} $$ Write a MATLAB program that request from the user when running the code to enter the value of the angle $\theta$ in degree, and then the program should check if the angle value is between $-20^{\circ}$ and $20^{\circ}$, and then calculates the relative intensity of the bright fringes. Note: $\theta_{\mathrm{rad}}=\theta_{\operatorname{deg}} \frac{ \pi}{180}$ Question #2: Write a MATLAB program to compute the sum of the series: $$ S=1+\frac{1}{x}+\frac{1}{x^{2}}+\frac{1} {x^{3}}+\cdots+\frac{1}{x^{r}} $$ The program when running the code should ask the user to enter the value of $x$ where $|x|>1$, and a positive value $r$. CS.PC.0021