Question 1-

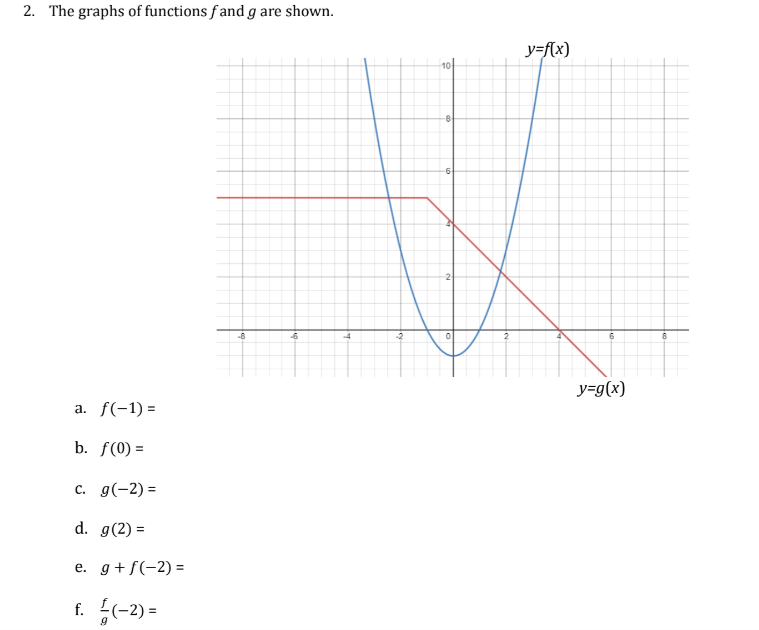
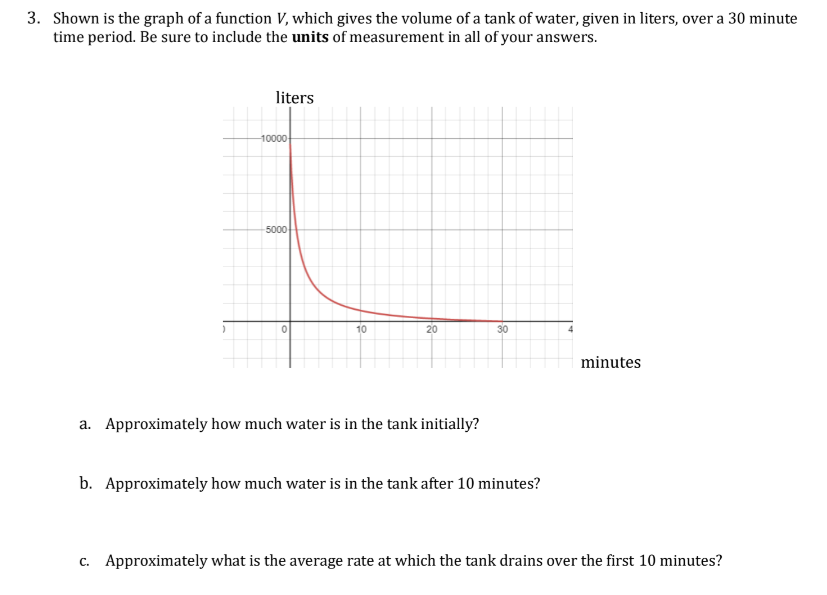
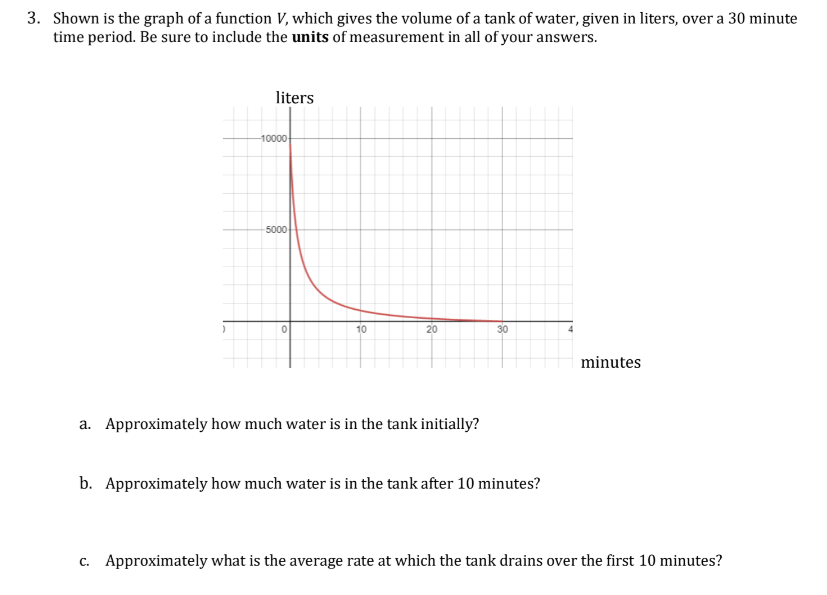
write. Whenever appropriate use interval notation. 1. Sketch the graph of a single function f that has all of the following properties. a. The domain of f is [-4, 4]. b. The range of f is [-5, 3]. C. f(2) = -1 d. f0?) = 2 e. f has exactlyr two local minimums and exactly one local maximum. For the function you have graphed above, estimate the following: i. Intervals of increase: ii. Intervals of decrease: iii. The local minimum values (these are y-values], and where they occur [this is an x-values]: iv. The local maximum Value, and where it occurs: \fg. All solutions to (x-values where) f(x) = g(x). Assume both graphs have domains of (-00, co). h. All solutions to (x-values where) f(x)