Question $1$xcos$($y$)$y$^(\text{'})=1+$sin$($y$).$

$($i$)$ Find the specific solution of this equation that satisfies the initial condition y$(1)=0.$

$($dy$)/($dx$)=(1)/($x$)*(1+$siny$)/($cosy$)=>($cosy$)/(1+$siny$)$dy$=(1)/($x$)$dx

$=>\backslash$int $($cosy$)/(1+$siny$)$dy$=\backslash$int $(1)/($x$)$dx$=>$ln$|1+$siny$|=$ln$|$x$|+$lnC

$=>|1+$siny$|=$C$|$x$|$

y$(1)=0|->|1+$sin$0|=$C$|1|=>$C$=1$

$=>|1+$siny$|=|$x$|$

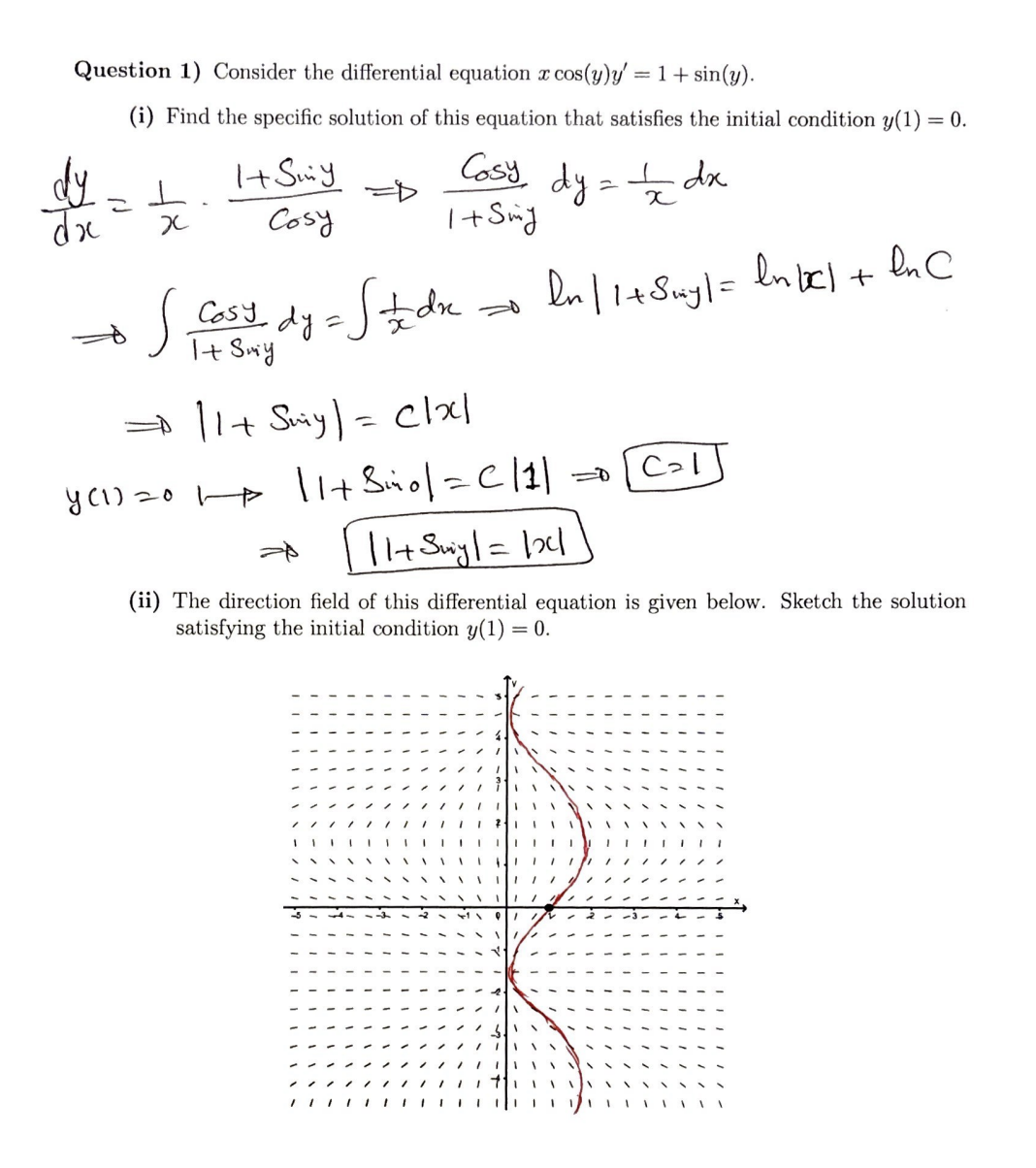
$($ii$)$ The direction field of this differential equation is given below. Sketch the solution

satisfying the initial condition y$(1)=0.$

i have this question im studying for an exam but im strugling with drawing the directional field if someone could show me in detials and explain the steps i have to take to do it would be highl apreicated