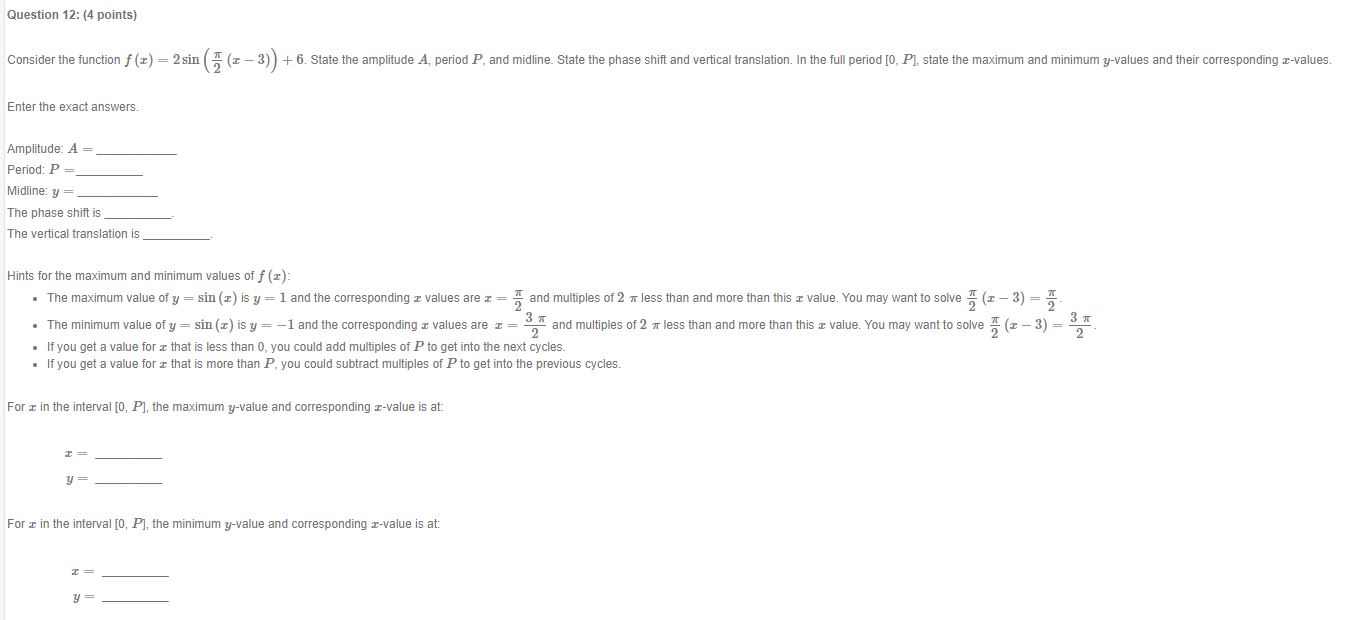
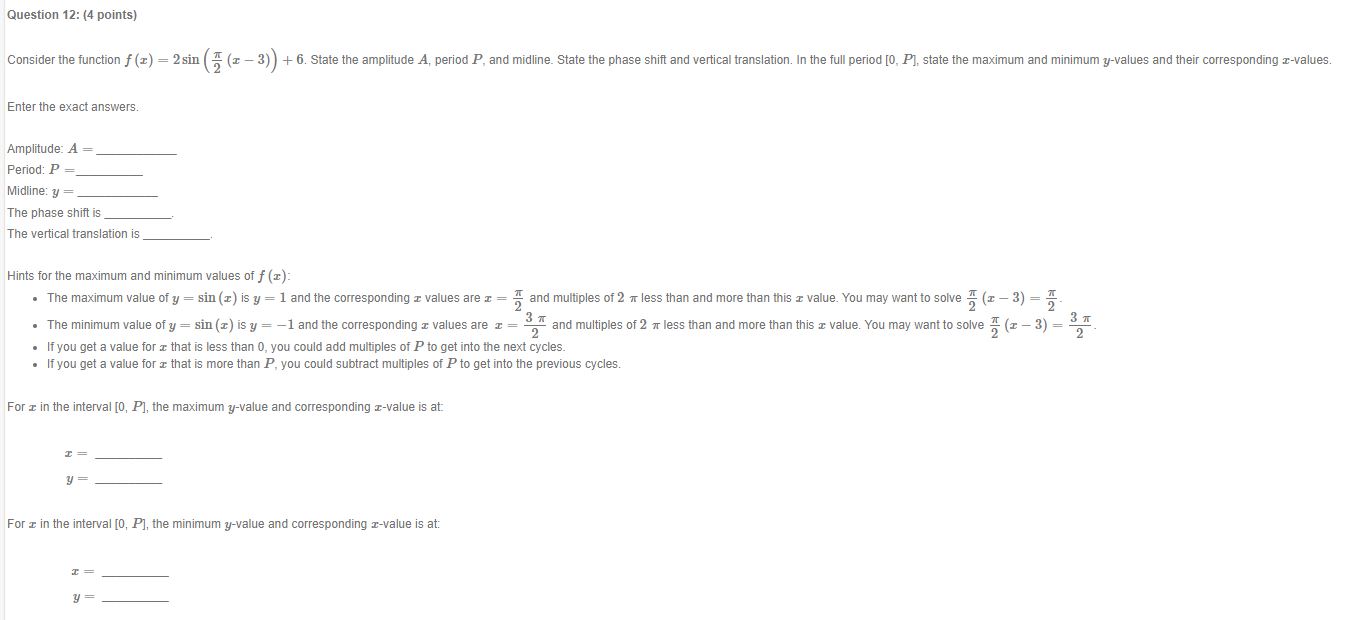
Question 12: (4 points) Consider the function f (z) = 2sin (x - 3) ) + 6. State the amplitude A, period P, and midline. State the phase shift and vertical translation. In the full period [0, P], state the maximum and minimum y-values and their corresponding z-values. Enter the exact answers. Amplitude: A = Period: P = Midline: y = The phase shift is The vertical translation is Hints for the maximum and minimum values of f (I): . The maximum value of y = sin (x) is y = 1 and the corresponding a values are z = - and multiples of 2 7 less than and more than this a value. You may want to solve " (x - 3) = . The minimum value of y = sin (x) is y = -1 and the corresponding r values are I = 3 1 2 and multiples of 2 7 less than and more than this I value. You may want to solve = (z - 3) = 3 1 2 . If you get a value for a that is less than 0, you could add multiples of P to get into the next cycles. . If you get a value for a that is more than P, you could subtract multiples of P to get into the previous cycles. For x in the interval [0, P], the maximum y-value and corresponding r-value is at: For z in the interval [0, P], the minimum y-value and corresponding z-value is at