question 15 following 7.3 example

thanks!

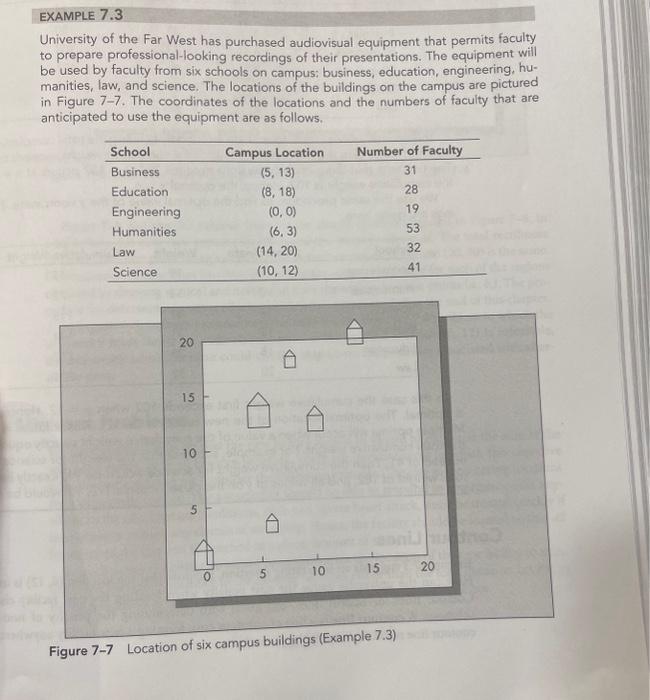
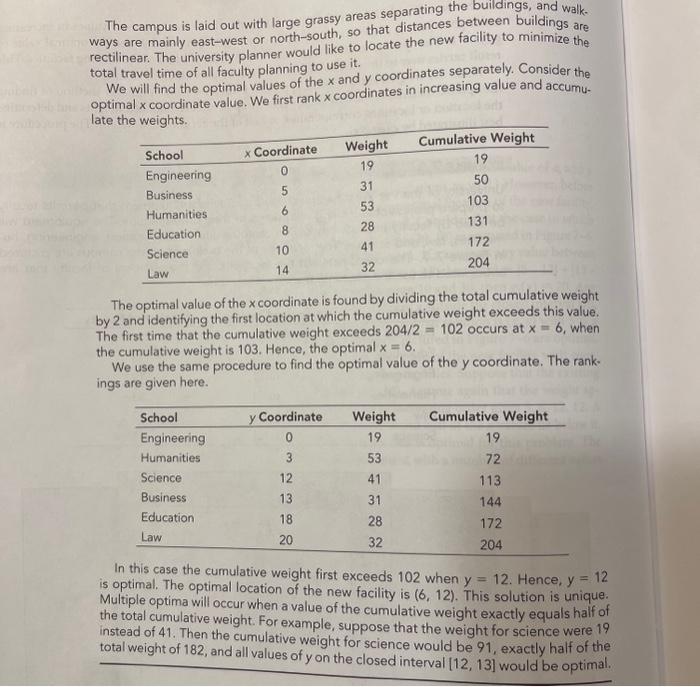
PROBLEMS FOR SECTION 7.3 15. A machine shop has five machines, located at (3,3),(3,7),(8,4),(12,3), and (14,6), respectively. A new machine is to be located in the shop with the following expected numbers of loads per hour transported to the existing machines: 81,81,41,1, and 61. Material is transported along parallel aisles, so a rectilinear distance measure is appro-priate. Find the coordinates of the optimal location of the new machine to minimize the weighted sum of the rectilinear distances from the new machine to the existing machines. EXAMPLE 7.3 University of the Far West has purchased audiovisual equipment that permits faculty to prepare professional-looking recordings of their presentations. The equipment will be used by faculty from six schools on campus; business, education, engineering, hu-manities, law, and science. The locations of the buildings on the campus are pictured in Figure 7-7. The coordinates of the locations and the numbers of faculty that are anticipated to use the equipment are as follows. Figure 7-7 Location of six campus buildings (Example 7.3) The campus is laid out with large grassy areas separating the buildings, and walk-ways are mainly east-west or north-south, so that distances between buildings are rectilinear. The university planner would like to locate the new facility to minimize the total travel time of all faculty planning to use it. We will find the optimal values of the x and y coordinates separately. Consider the optimal x coordinate value. We first rank x coordinates in increasing value and accumu. late the weights. The optimal value of the x coordinate is found by dividing the total cumulative weight by 2 and identifying the first location at which the cumulative weight exceeds this value. The first time that the cumulative weight exceeds 204/2=102 occurs at x=6, when the cumulative weight is 103 . Hence, the optimal x=6. We use the same procedure to find the optimal value of the y coordinate. The rank-ings are given here. In this case the cumulative weight first exceeds 102 when y=12. Hence, y=12 is optimal. The optimal location of the new facility is (6,12). This solution is unique. Multiple optima will occur when a value of the cumulative weight exactly equals half of the total cumulative weight. For example, suppose that the weight for science were 19 instead of 41. Then the cumulative weight for science would be 91, exactly half of the total weight of 182 , and all values of y on the closed interval [12,13] would be optimal