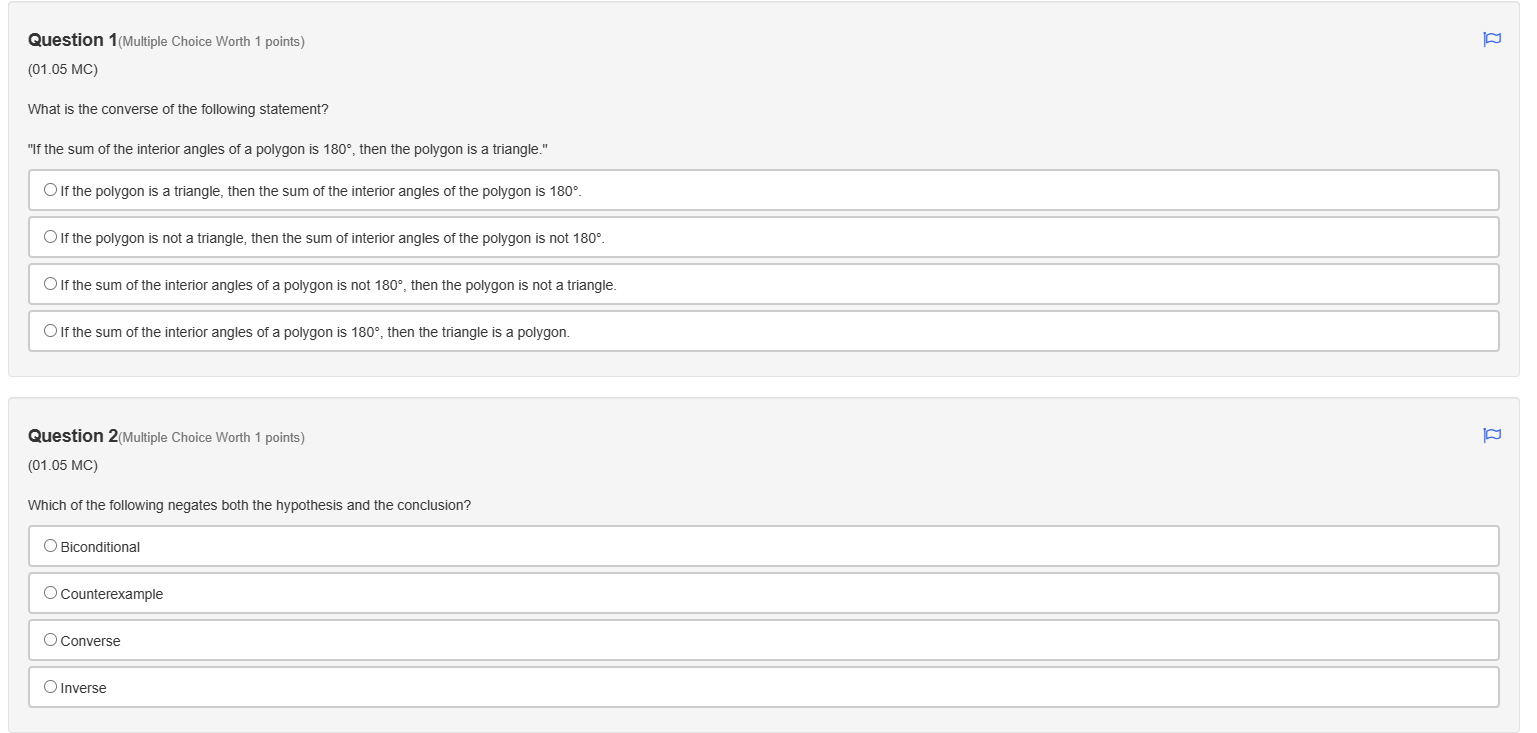
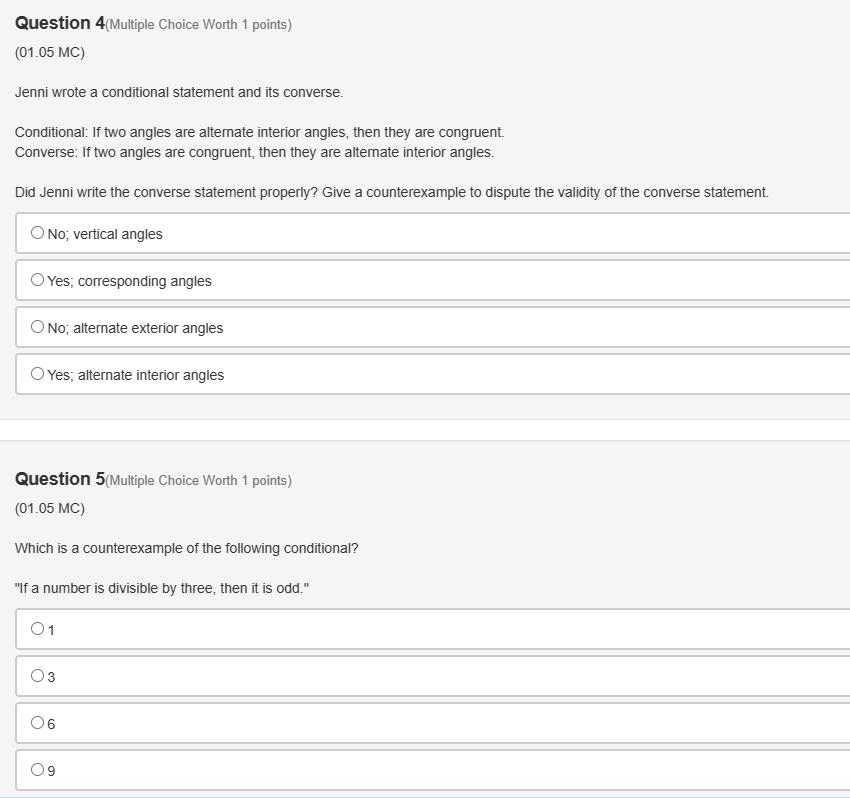
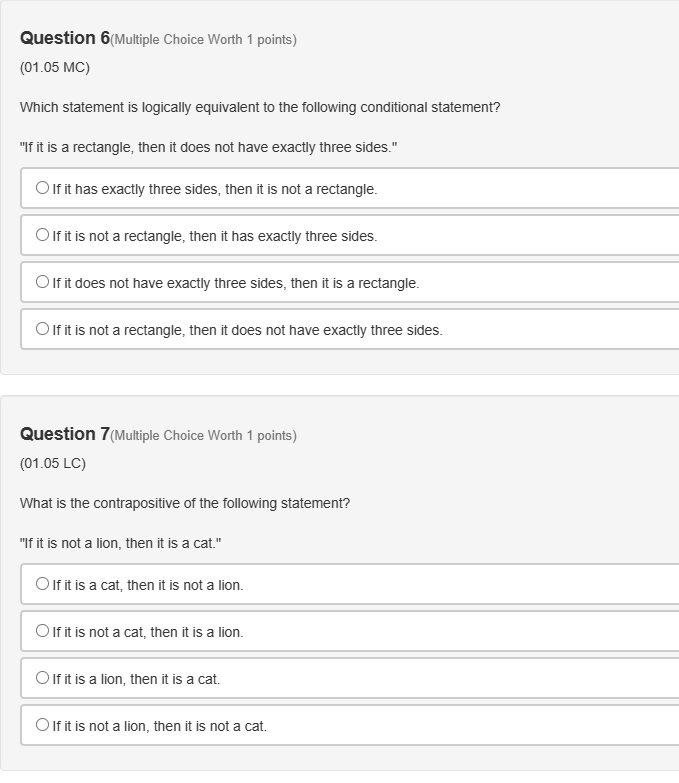
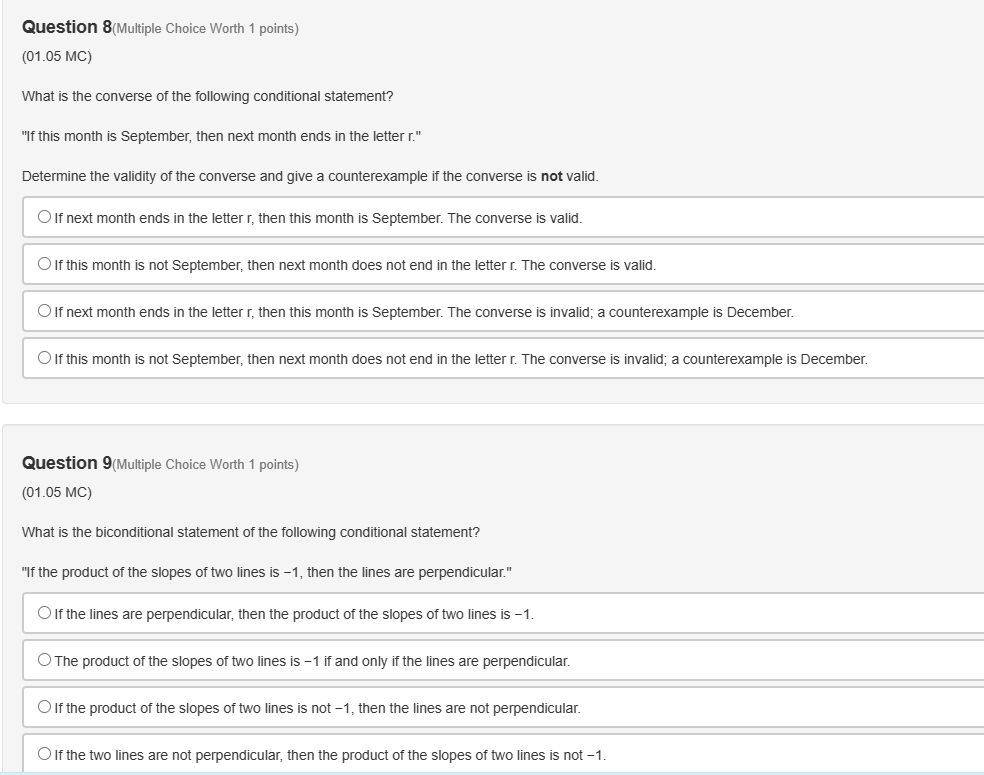
Question 1(Multiple Choice Worth 1 points) (01.05 MC) What is the converse of the following statement? "If the sum of the interior angles of a polygon is 180, then the polygon is a triangle." O If the polygon is a triangle, then the sum of the interior angles of the polygon is 180. O If the polygon is not a triangle, then the sum of interior angles of the polygon is not 180. If the sum of the interior angles of a polygon is not 180, then the polygon is not a triangle. If the sum of the interior angles of a polygon is 180, then the triangle is a polygon. Question 2(Multiple Choice Worth 1 points) (01.05 MC) Which of the following negates both the hypothesis and the conclusion? O Biconditional O Counterexample O Converse O InverseQuestion 10(Multiple Choice Worth 1 points) (01.05 LC) What is the inverse of the following statement? "If a polygon does not have five sides, then the polygon is a rectangle." O If the polygon is a rectangle, then the polygon does not have five sides. O If the polygon is not a rectangle, then the polygon has five sides. O If the polygon does not have five sides, then the polygon is not a rectangle. If the polygon has five sides, then the polygon is not a rectangle.Question 3(Multiple Choice Worth 1 points) (01.05 MC) Read the following statements. Statement 1: "If she is stuck in traffic, then she is late." Statement 2: "If she is late, then she is stuck in traffic." Statement 3: "If she is not late, then she is not stuck in traffic." Sue writes, "Statement 2 is the converse of statement 3 and contrapositive of statement 1." Kim writes, "Statement 1 is the inverse of statement 2 and converse of statement 3." Who is correct? O Only Kim is correct. O Both Sue and Kim are correct. O Both Sue and Kim are incorrect. O Only Sue is correct.Question 4(Multiple Choice Worth 1 points) (01.05 MC) Jenni wrote a conditional statement and its converse. Conditional: If two angles are alternate interior angles, then they are congruent. Converse: If two angles are congruent, then they are alternate interior angles. Did Jenni write the converse statement properly? Give a counterexample to dispute the validity of the converse statement. O No; vertical angles Yes; corresponding angles O No; alternate exterior angles O Yes; alternate interior angles Question 5(Multiple Choice Worth 1 points) (01.05 MC) Which is a counterexample of the following conditional? "If a number is divisible by three, then it is odd." 01 06 09Question 6(Multiple Choice Worth 1 points) (01.05 MC) Which statement is logically equivalent to the following conditional statement? "If it is a rectangle, then it does not have exactly three sides." If it has exactly three sides, then it is not a rectangle. If it is not a rectangle, then it has exactly three sides. O If it does not have exactly three sides, then it is a rectangle. O If it is not a rectangle, then it does not have exactly three sides. Question 7(Multiple Choice Worth 1 points) (01.05 LC) What is the contrapositive of the following statement? "If it is not a lion, then it is a cat." If it is a cat, then it is not a lion. O If it is not a cat, then it is a lion. If it is a lion, then it is a cat. O If it is not a lion, then it is not a cat.Question 8(Multiple Choice Worth 1 points) (01.05 MC) What is the converse of the following conditional statement? "If this month is September, then next month ends in the letter r." Determine the validity of the converse and give a counterexample if the converse is not valid. O If next month ends in the letter r, then this month is September. The converse is valid. If this month is not September, then next month does not end in the letter r. The converse is valid. OIf next month ends in the letter r, then this month is September. The converse is invalid; a counterexample is December. O If this month is not September, then next month does not end in the letter r. The converse is invalid; a counterexample is December. Question 9(Multiple Choice Worth 1 points) (01.05 MC) What is the biconditional statement of the following conditional statement? "If the product of the slopes of two lines is -1, then the lines are perpendicular." O If the lines are perpendicular, then the product of the slopes of two lines is -1. O The product of the slopes of two lines is -1 if and only if the lines are perpendicular. If the product of the slopes of two lines is not -1, then the lines are not perpendicular. O If the two lines are not perpendicular, then the product of the slopes of two lines is not -1