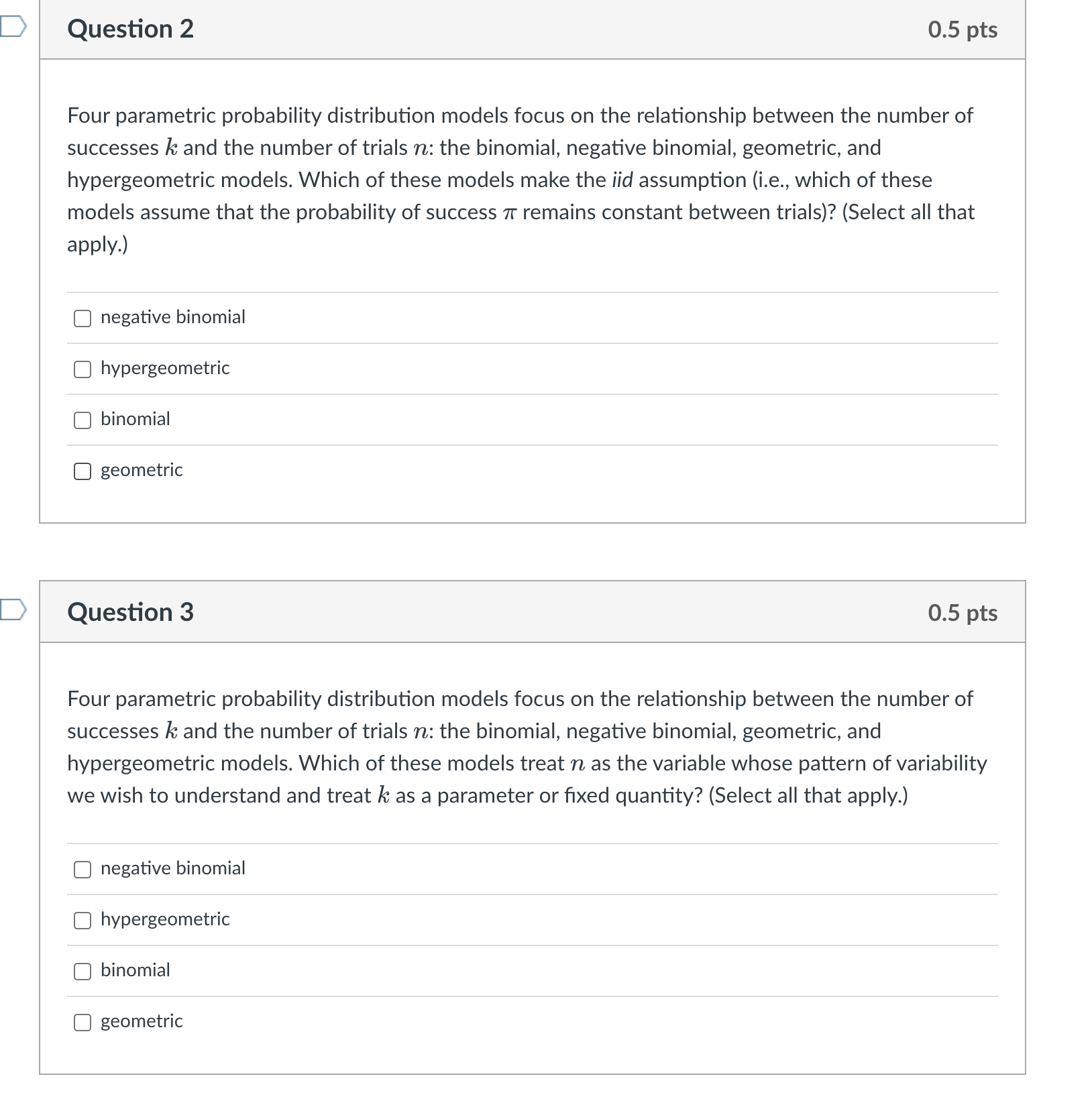
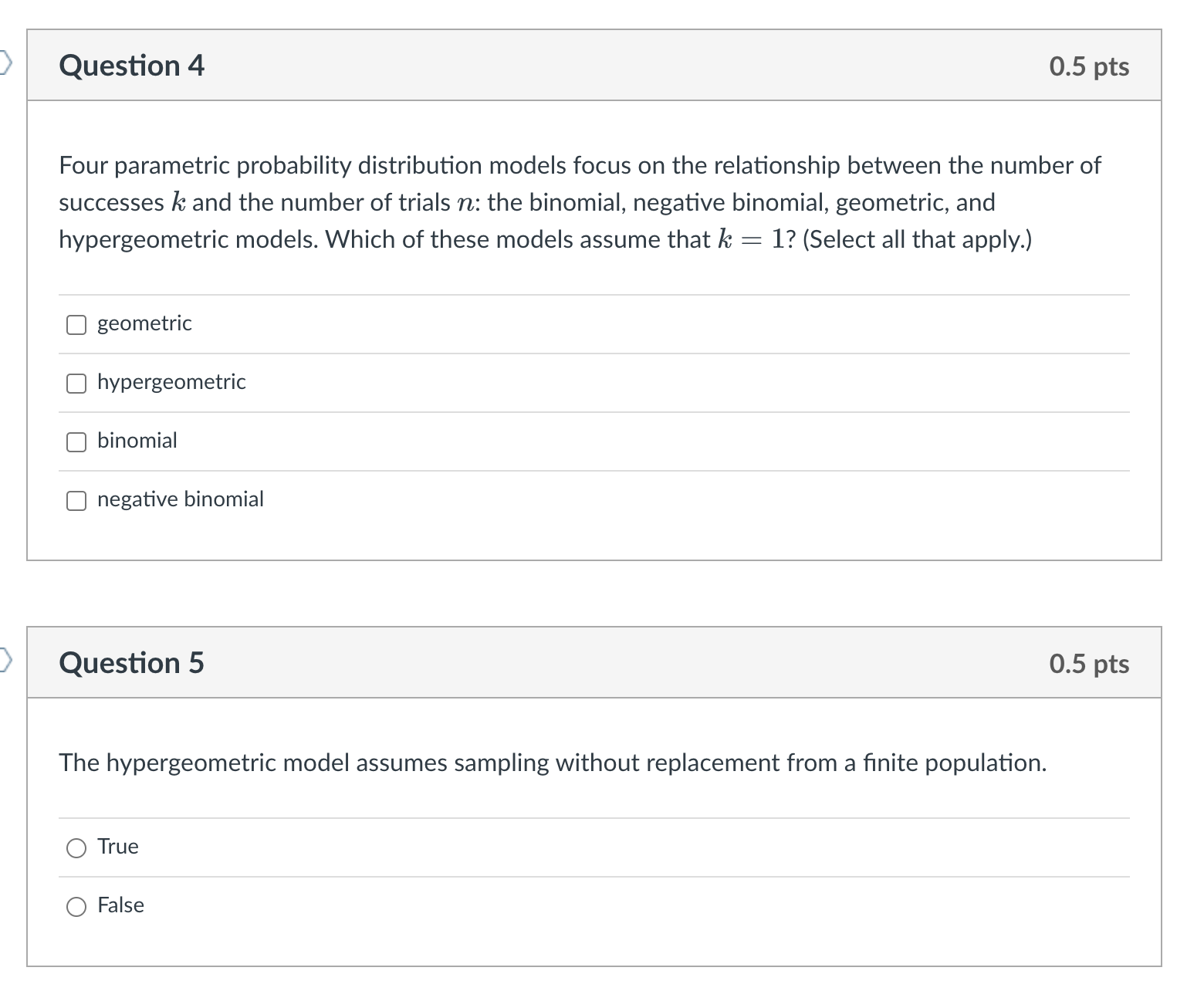
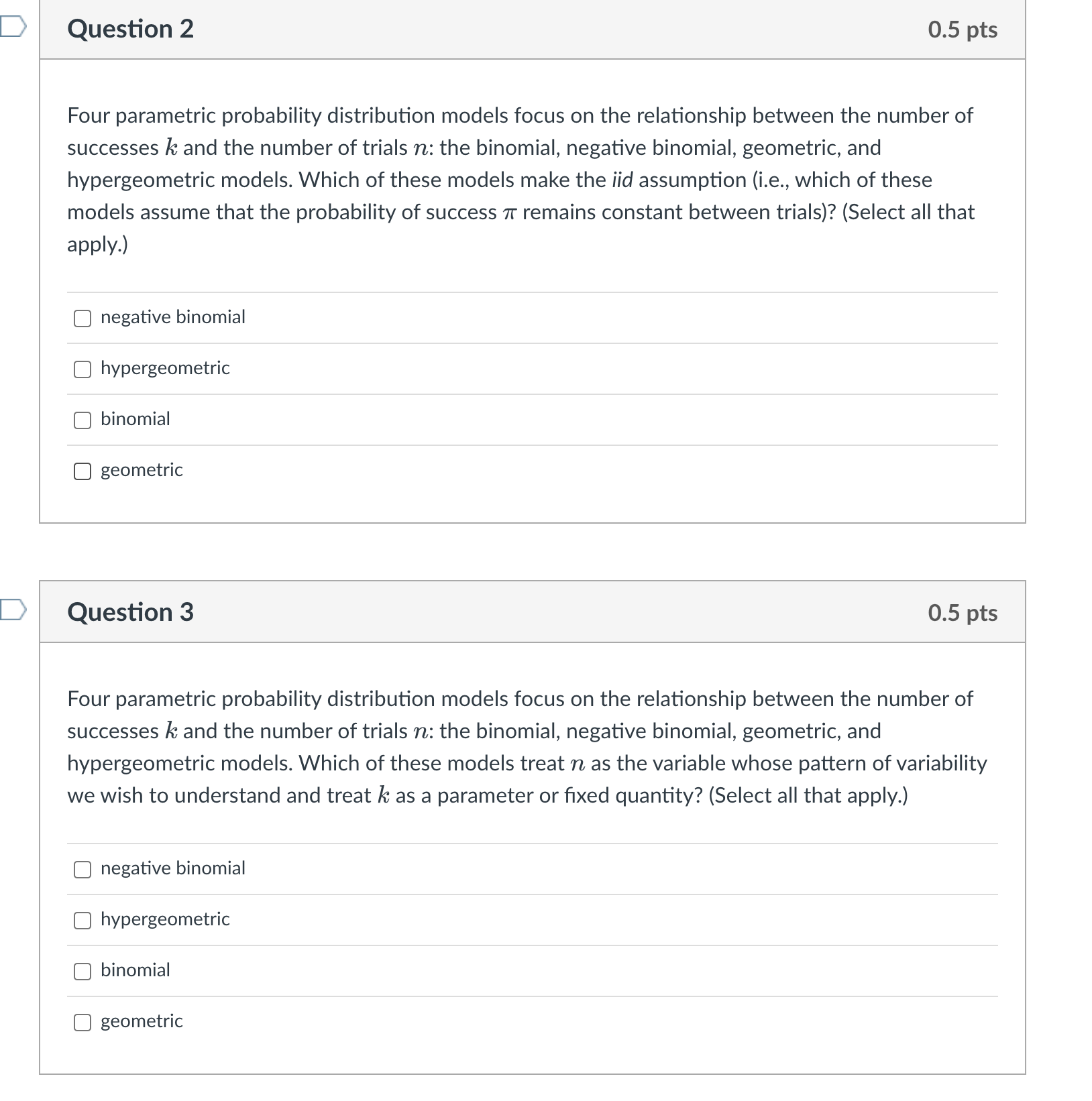
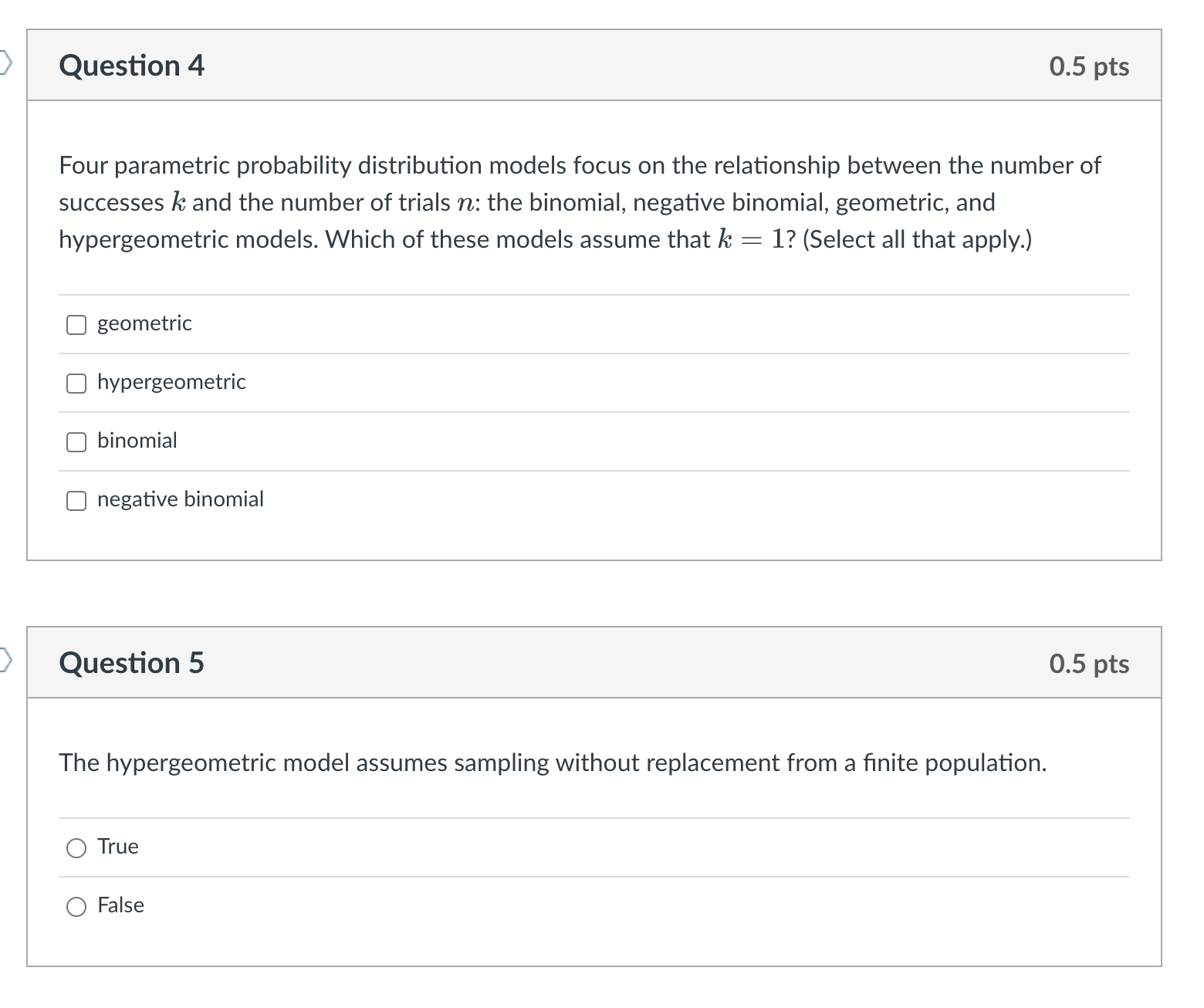
Question 2 0.5 pts Four parametric probability distribution models focus on the relationship between the number of successes k and the number of trials 77.: the binomial, negative binomial, geometric, and hypergeometric models. Which of these models make the iid assumption (i.e., which of these models assume that the probability of success 11' remains constant between trials)? (Select all that apply.) C] negative binomial C] hypergeometric C] binomial C] geometric Question 3 0.5 pts Four parametric probability distribution models focus on the relationship between the number of successes k and the number of trials 77.: the binomial, negative binomial, geometric, and hypergeometric models. Which of these models treat 77. as the variable whose pattern of variability we wish to understand and treat k as a parameter or xed quantity? (Select all that apply.) C] negative binomial C] hypergeometric C] binomial C] geometric ) Question 4 0.5 pts Four parametric probability distribution models focus on the relationship between the number of successes k and the number of trials 12: the binomial, negative binomial, geometric, and hypergeometric models. Which of these models assume that k = 1? (Select all that apply.) C] geometric C] hypergeometric C] binomial C] negative binomial Question 5 0.5 pts The hypergeometric model assumes sampling without replacement from a nite population. 0 True 0 False