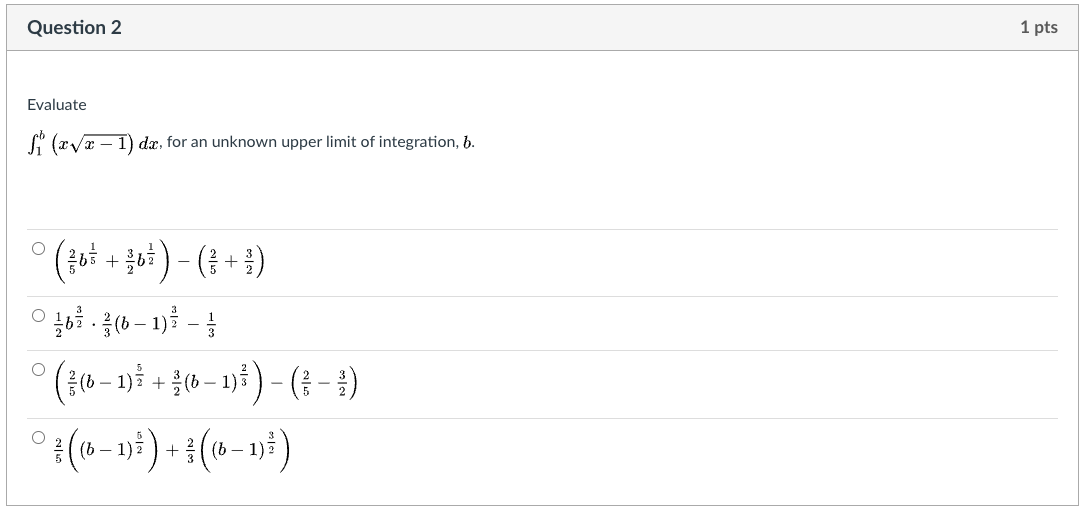
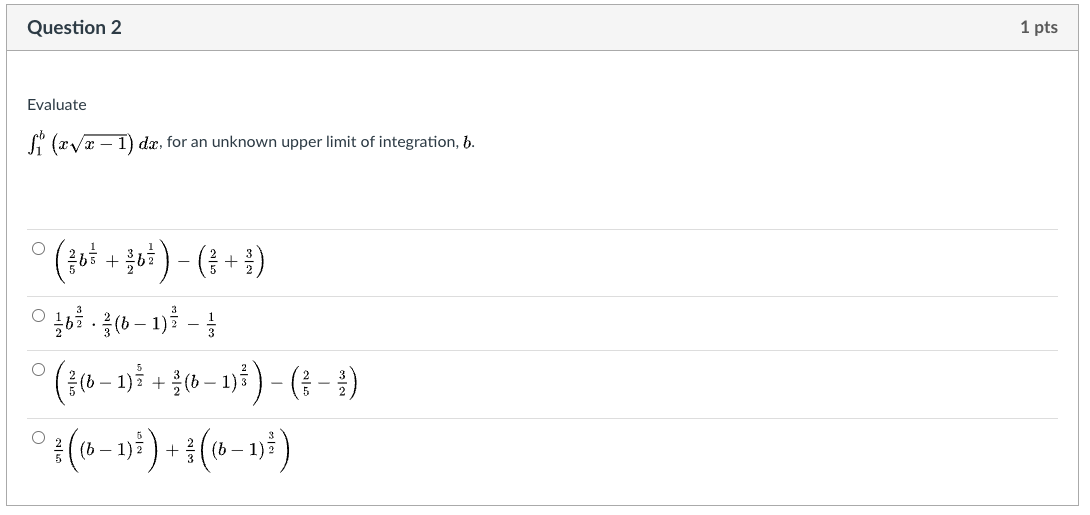
Question: Question 2 1 pts Evaluate (*Vx - 1) da, for an unknown upper limit of integration, b. O b5 + 19/00 10/ 40 - +
![[ Select ] . The biggest reason we choose that approach is](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666813f688d22_886666813f6795ab.jpg)
![because there is a [ Select ] in the integrand. We let](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666813f6cb106_886666813f6bac43.jpg)
![[ Select ] - 2, and we let [ Select ] 6x3](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666813f732119_887666813f711f14.jpg)
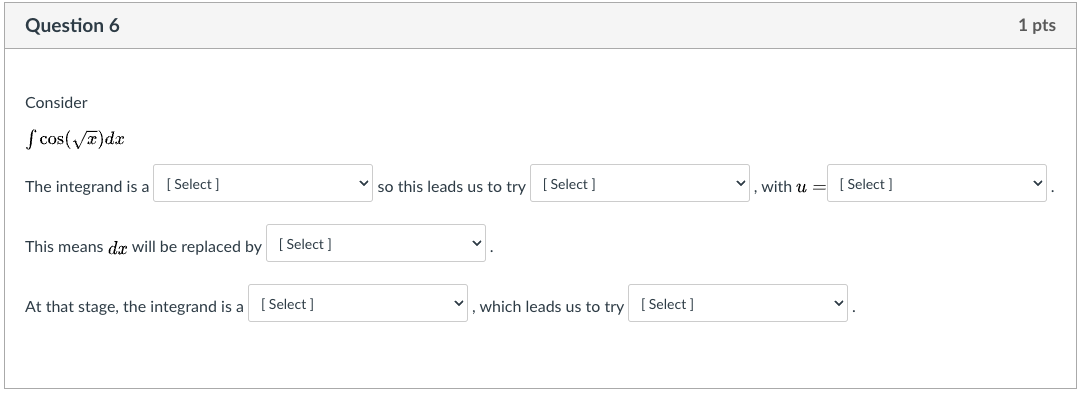
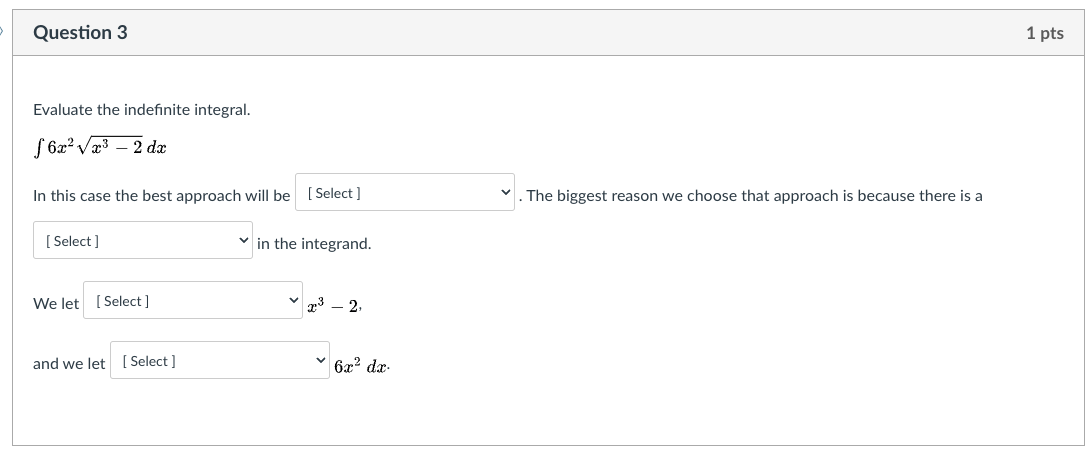
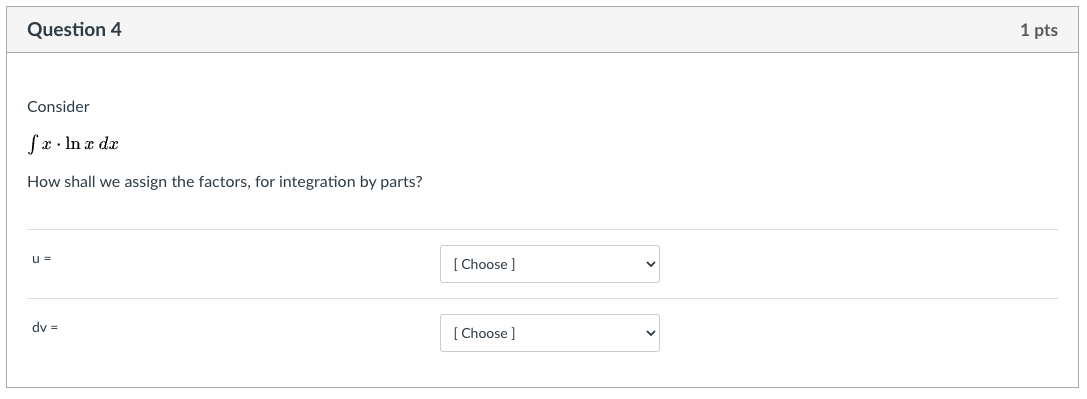
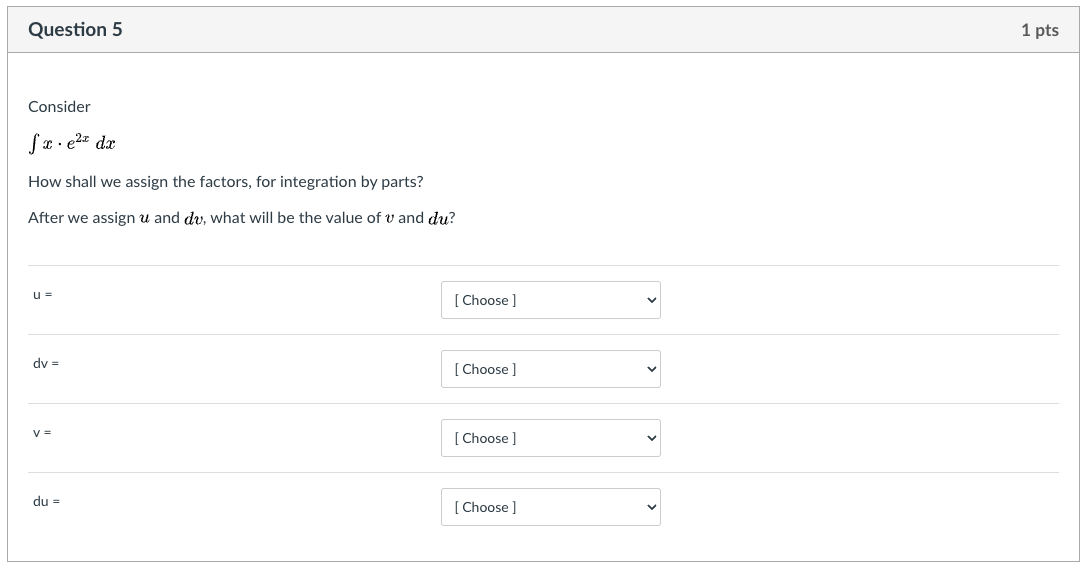
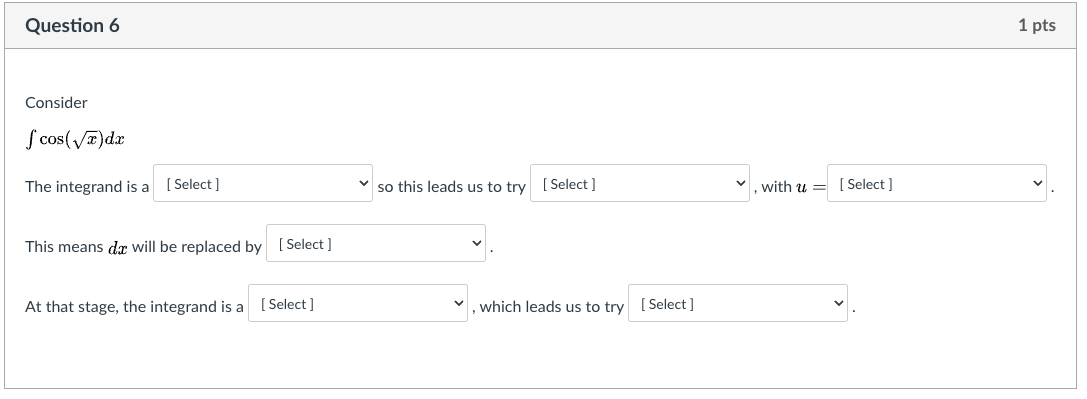
Question 2 1 pts Evaluate (*Vx - 1) da, for an unknown upper limit of integration, b. O b5 + 19/00 10/ 40 - + O -bi . (b - 1) - O (6 - 1)1 + $16 -1) | N - (3 - 2) O (b - 1)7 (b- 1)Question 3 1 pts Evaluate the indefinite integral. 6x2 vx3 - 2 dx In this case the best approach will be [ Select ] . The biggest reason we choose that approach is because there is a [ Select ] in the integrand. We let [ Select ] - 2, and we let [ Select ] 6x3 dx.Question 4 1 pts Consider fx . Incdx How shall we assign the factors, for integration by parts? U = [ Choose ] v dv = [ Choose ] vQuestion 5 1 pts Consider f a: - eh (in: How shall we assign the factors, for integration by parts? After we assign 1.6 and day. what will be the value of v and (in? u = [ Choose ] dv = [ Choose ] V = [ Choose ] d\" = [ Choose ] Question 6 1 pts Consider f cos( vx)dx The integrand is a [ Select ] so this leads us to try [ Select ] , with u = [ Select ] This means da will be replaced by [ Select ] At that stage, the integrand is a [ Select ] , which leads us to try |[ Select ]
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


