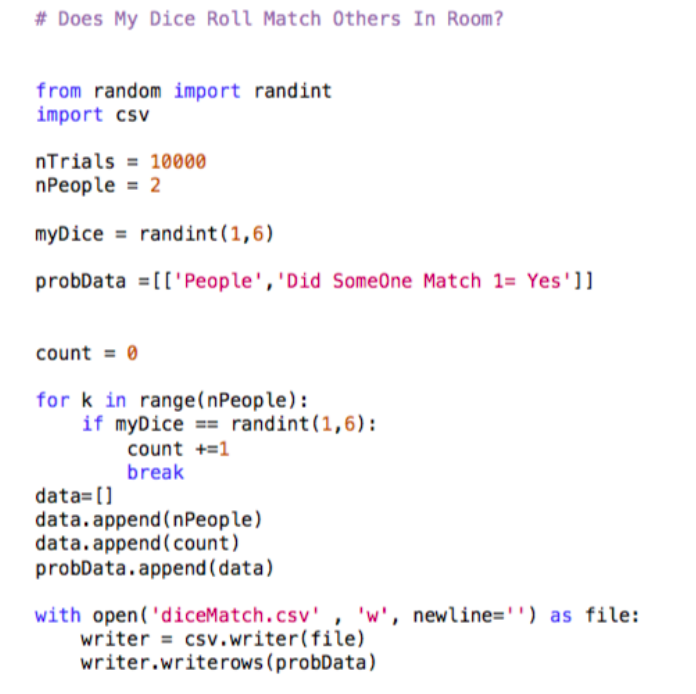
Question 2: (25 points) My Birthday. Consider the case where you are in the room with M randomly selected people. You would like to estimate the probability that at least one person in the room has the same birthday as yours. One way to conduct the experiment is to survey groups of M people throughout the UAH campus. Each time a group is interviewed, you record if there is someone with your birthday. Your estimate for the probability that someone has your birthday in a group of M people is the ratio of the number of times the survey finds a person with your birthday (Nsuccess), to the number of trials (Ntrials). That is Nsuccess/Ntrials. You will have a better estimate if you survey is conducted with a more significant number of trials Ntrials >1,000. The experiment is time consuming to perform. It also becomes more time-consuming as the test is run for different numbers of M people for which the probability is being evaluated Python offers an economical way to simulate the experiment using the random number generation facilities inherent in the programming language, using the Monte Carlo technique Design a simulation by importing the random module into Python. Specifically, from random import randint. Design your simulation first to select your birthday using the assignment myBirthday = randm(1,365). Assume that there are no leap years (i.e., there are only 365 days in a year). Write a well-documented Python program, the main program, that prompts the user for the Number of People in the room Finally, within the main program, estimate the probability someone having your same birthday with the user-defined number of people. Initially, assume that no one has the same birthday by setting a counter equal to zero. The counter gets incremented by one if any person in the room has the same birthday as yours On a single trial, with a user input 200 people, you may not find someone with your birthday. If you manually rerun the simulation ten times, your code, however, should see that approximately four (4.22 exactly) times there is a match to your birthday. Simulating with more people, say 400, will on average produce a match to your birthday about seven times (6.66 exactly) in ten trials. Submit your code in a text file labeled single Trial.py. Hints: Consider the case where you want to find out if anyone in the room has rolled the same value on a six-sided die? How would you structure that code (see below)