Question: Question 2 ( 4 5 points ) Two cases for crack propagation relating to the Griffith Energy Balance were shown in lectures: ( 1 )
Question points
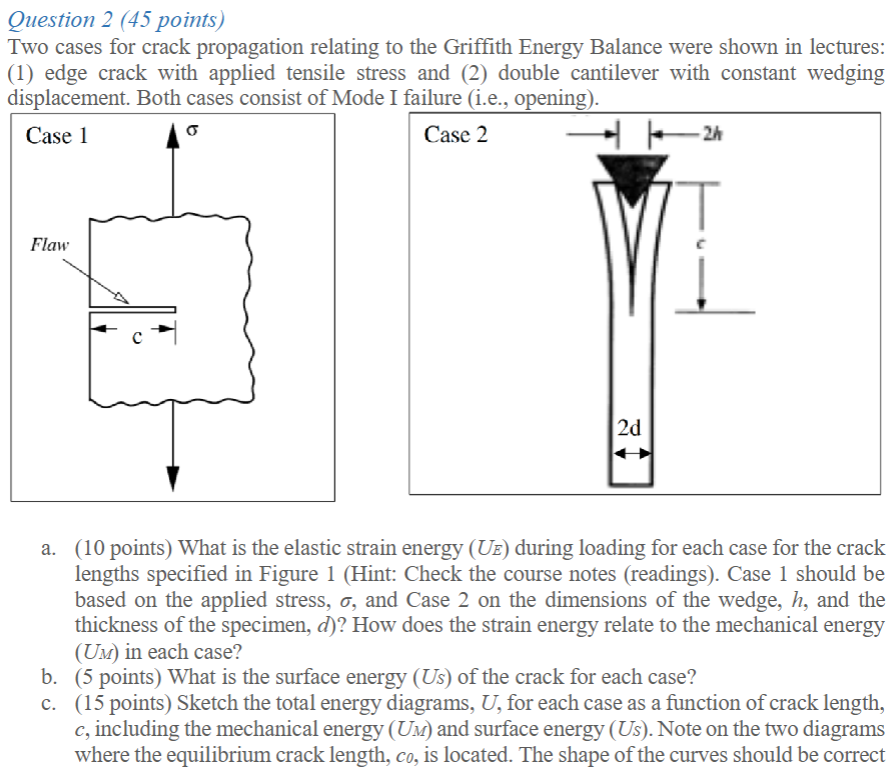
Two cases for crack propagation relating to the Griffith Energy Balance were shown in lectures:
edge crack with applied tensile stress and double cantilever with constant wedging
displacement. Both cases consist of Mode I failure ie opening
a points What is the elastic strain energy UE during loading for each case for the crack
lengths specified in Figure Hint: Check the course notes readings Case should be
based on the applied stress, sigma, and Case on the dimensions of the wedge, h and the
thickness of the specimen, d How does the strain energy relate to the mechanical energy
UM in each case?
b points What is the surface energy Us of the crack for each case?
c points Sketch the total energy diagrams, U for each case as a function of crack length,
c including the mechanical energy UM and surface energy Us Note on the two diagrams
where the equilibrium crack length, c is located. The shape of the curves should be correct
points For each case, derive the equilibrium crack length, cc in terms of i the
applied stress for Case and ii the wedge dimensions for Case
e points For each case, is this equilibrium crack length, c stable or unstable? Explain
your answer. d points For each case, derive the equilibrium crack length, cc in terms of i the applied stress sigma for Case and ii the wedge dimensions for Case
e points For each case, is this equilibrium crack length, co stable or unstable? Explain your answer.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


