Question: Question 2 (9 marks) Let (fn), fn : [a, b] - R be a sequence of functions. Assume that fn converges uniformly to a function
![Question 2 (9 marks) Let (fn), fn : [a, b] -](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6709d90c0abf6_6356709d90be4847.jpg)
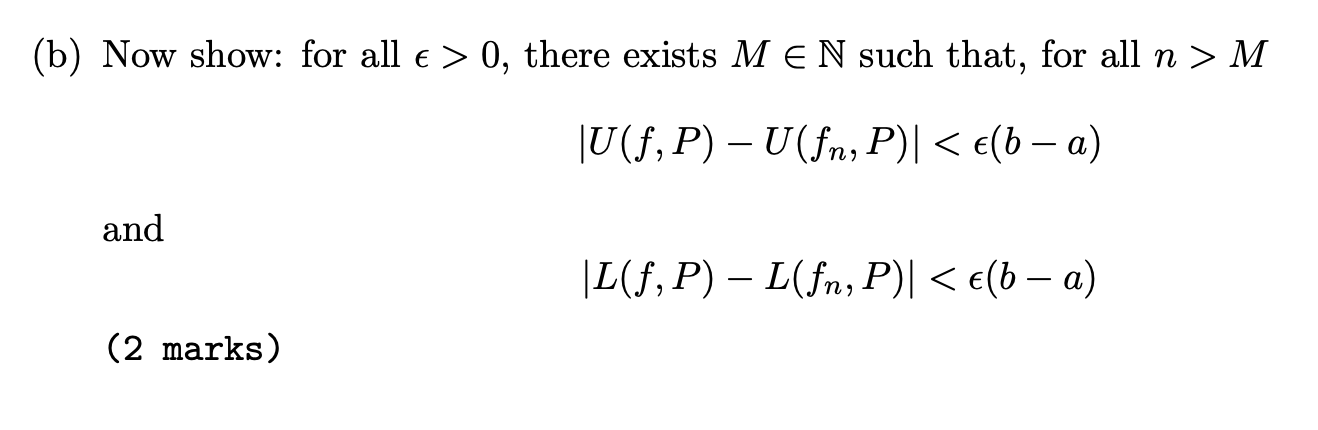
![a function f : [a, b] -> R, and that each function](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6709d90cdb2f1_6366709d90cc865a.jpg)
Question 2 (9 marks) Let (fn), fn : [a, b] - R be a sequence of functions. Assume that fn converges uniformly to a function f : [a, b] -> R, and that each function fn is Riemann integrable. (a) Let P = {a = x0 0, there exists M E N such that, when n > M Imx - MK/ KE and I MK - MPIKE (4 marks)(b) Now show: for all e > 0, there exists M E N such that, for all n > M JU(f, P) - U(fn, P) |
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


