Question $2$

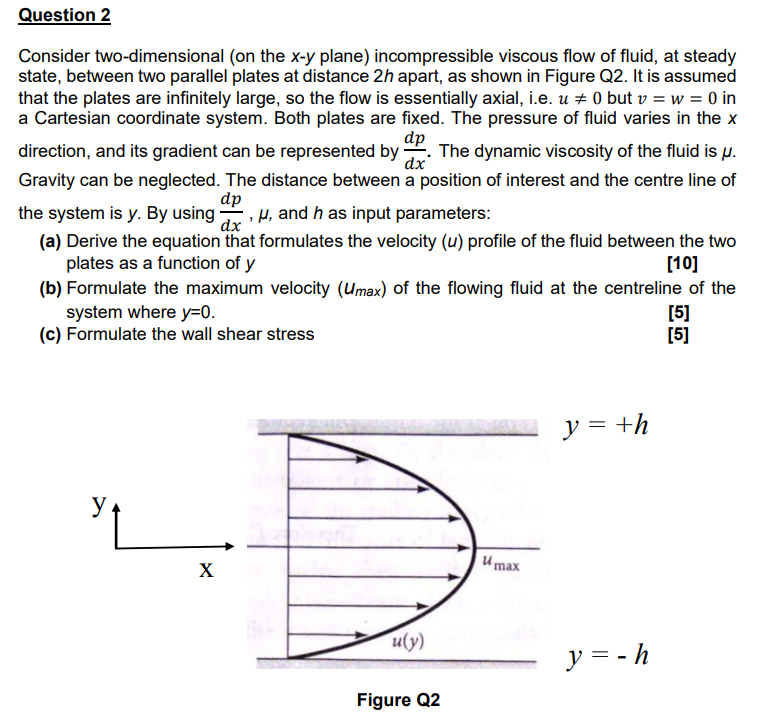
Consider two$-$dimensional $($on the $\backslash ($ x$-$y $\backslash )$ plane$)$ incompressible viscous flow of fluid, at steady state, between two parallel plates at distance $\backslash (2$ h $\backslash )$ apart, as shown in Figure Q$2.$ It is assumed that the plates are infinitely large, so the flow is essentially axial, i$.$e$.\backslash ($ u

eq $0\backslash )$ but $\backslash ($ v$=$w$=0\backslash )$ in a Cartesian coordinate system. Both plates are fixed. The pressure of fluid varies in the $\backslash ($ x $\backslash )$ direction, and its gradient can be represented by $\backslash (\backslash$frac$\{$d p$\}\{$d x$\}\backslash ).$ The dynamic viscosity of the fluid is $\backslash (\backslash$mu $\backslash ).$ Gravity can be neglected. The distance between a position of interest and the centre line of the system is $\backslash ($ y $\backslash ).$ By using $\backslash (\backslash$frac$\{$d p$\}\{$d x$\},\backslash$mu $\backslash ),$ and $\backslash ($ h $\backslash )$ as input parameters:

$($a$)$ Derive the equation that formulates the velocity $\backslash (($u$)\backslash )$ profile of the fluid between the two plates as a function of $\backslash ($ y $\backslash )$

$($b$)$ Formulate the maximum velocity $(\backslash ($ u$\_\{\backslash$max $\}\backslash ))$ of the flowing fluid at the centreline of the system where $\backslash ($ y$=0\backslash ).$

$($c$)$ Formulate the wall shear stress

Figure Q$2$