Question: Question # 2: Construct the solution for the given partial differential equation on initial and boundary conditions, by separation of variables (use Fourier series

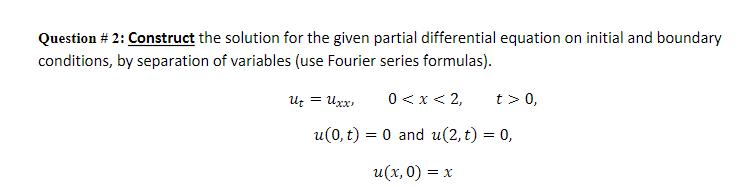
Question # 2: Construct the solution for the given partial differential equation

Question # 2: Construct the solution for the given partial differential equation on initial and boundary conditions, by separation of variables (use Fourier series formulas). Ut = Uxx 0 < x < 2, t > 0, u(0, t) = 0 and u(2, t) = 0, u(x, 0) = = x

Step by Step Solution

★★★★★

3.28 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

using separation of variables we have UtUxx UtTxx where UxtTxt Therefore TxxTtt This is the wave ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Electrical Engineering Questions!

Use separation of variables to solve the following autonomous differential equations. Check your answers by differentiating. db dt = 0.011, b(0) = 1000.

Use separation of variables to solve the following pure-time differential equations. Check your answers by differentiating. d L = 64.3e-1.19t, with L (0) = 0 dt

Use separation of variables to solve the following autonomous differential equations. Check your answers by differentiating. 3,b(0)-1.0x 10

In Problems 1 through 12 first solve the equation f (x) = 0 to find the critical points of the given autonomous differential equation dx/dt = f (x) Then analyze the sign of f (x) to determine whether...

In Problems 9 through 12, find each equilibrium solution x(t) x 0 of the given second-order differential equation x" + f(x , x') = 0. Use a computer system or graphing calculator to construct a...

verify that the indicated function y = (x) is an explicit solution of the given first-orde differential equation. Proceed as in Example 2, by considering simply as a function, give its domain. Then...

A standard model for describing the dispersion of chemical pollutants in the atmosphere is the Gaussian plume model. In this model it is assumed that the wind carries the pollutant in the $x$...

Approximate the solution to the following partial differential equation using the Backward-Difference method. u / t 2u / x2 = 0, 0

Firm Prospect Inc. does not pay any dividend now and is expected to start paying dividend of $5 per share exactly TWO years from today. The dividend is also expected to grow at a constant rate 5%...

As an accounting associate director of Sunlight Office Supplies, you have been asked to create a memo to sales managers showing the second quarter sales figures by category. The memo should contain a...

Seating arrangements and food preparation process at Benihana restaurants encourage interactions among total strangers, as well as contacts between patrons and the Japanese chef who prepares their...

The stock of MTY Golf World currently sells for $80 per share. The firm has a constant dividend growth rate of 6% and is expected to pay a dividend of $4.80. If the required rate of return is 12%,...

The company president is Vincent Miller, who inherited the company. When the company was founded over 30 years ago, it originally focuses on producing high-end batteries, for automobile...

show work Scenario A: Jane purchased a new car for $15,000. She financed it with a 60 month fixed installment loan with an APR of 5.0% Determine the finance charge and the monthly payment. Scenario...

show working pls 3 5 points eBook Print References Goldstream Enterprises has bonds on the market making annual payments, with nine years to maturity, and selling for $948. At this price, the bonds...

The following data are supplied for the common stocks of Nikola Corporation, Tesla, Inc. and General Motors: Nikola Corp (NKLA) Tesla Inc. (TSLA) Close Price ($) Close Price ($) 67.53 30.00 40.81...

Find the ordinary differential equation relating a current source i s (t) = cos(? 0 t) with the current i L (t) in an inductor, with inductance L = 1 Henry, connected in parallel with a resistor of R...

Let y(t) = dx(t)/dt, where x(t) = 4cos(2t),

The following problems are about energy and power of signals. (a) Plot the signal x(t) = e t u(t) and determine its energy. What is the power of x(t)? (b) How does the energy of z(t) = e £ t...

Explain the action potential.

Recall the role of various endocrine glands.

Identify the parts of a neuron and describe the function of each.