**Question 2 is the question paper that I received with no reference given. However, I did attach some sample notes for reference.

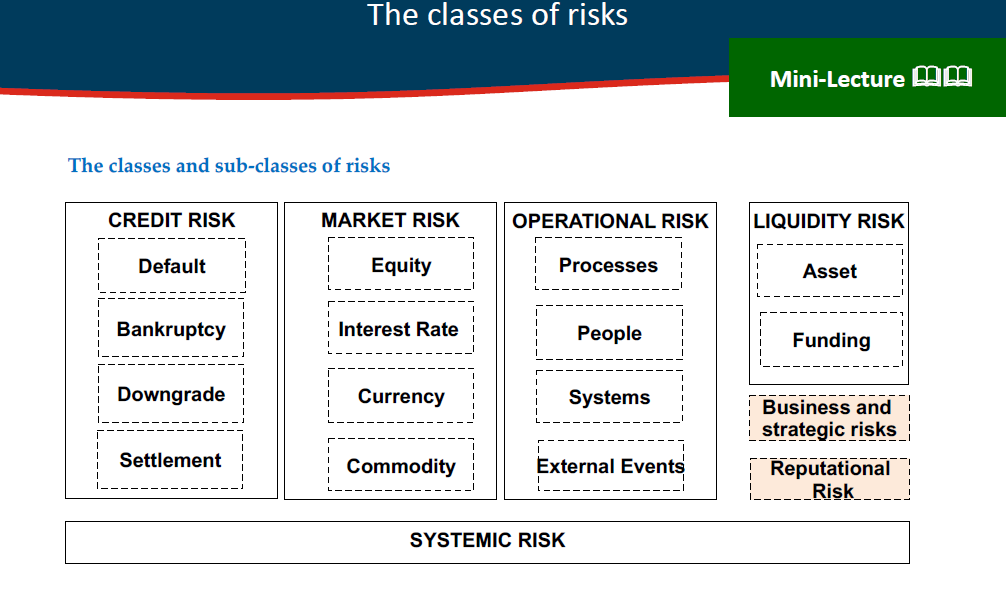
\fQuestion 2 A rm holds a bond with a value of $1 50 million and an estimated probability of default of 4% over the coming 12 months. The policyr of the lm sets its risk Limit to 95% VaR (Value at Risk} and 95% ES (expected shortfall) for an}r individual security. Assume the bond bears E risk of loss due changes in the market price g in the traded value. (a) Categorise the exact class of risk to which the bond is exposed here. (3 marks) (1')) Compute the 95% VaR measure for this bond and explain your result. (T marks) (c) Compute the 95% ES measure for this bond and explain your result. (10 marks) (d) Assume now that the condence level is increased to 99% on both hmits. Compute the new VaR and ES measures and explain your results. (5 marks) 1. Each of two independent projects has a probability 0.98 of a loss of $1 million and 0.02 probability of a loss of $10 million a) What is the 97.5% VaR for each project? 97.5% falls within the rst 98% range. The 97.5% VaR is therefore $1 million. b) What is the 97.5% expected shortfall for each project? The E3 is the average loss in the 2.5% tail, which includes the worst 2.0% + the next worst 0.5%. ES is therefore $10 million at 272.5 + $1 million x 0.5.12.5 = $8.2 million. 0) What is the 97.5% VaR for the portfolio? The portfolio of two independent projects is the result of combined probabilities. The portfolio has 0.98 x 0.98 = 0.9604 probability of $2 million loss, 0.98 x 0.02 +0.02 x 0.98 = 0.0392 probability of $11 million loss, and 0.02 x 0.02 = 0.0004 chance of $20 million loss. The 97.5% VaR is therefore $11 million as 97.5% lies in the 09604-09996 range of $11 million. d) What is the 97.5% expected shortfall for the portfolio? The E3 is 0000470025 x320 million + (0.025 -0.0004)!0.025 x $11 million.= $10324 million. The definition VaR tells you: - \"What loss level is such that - we are X% confident it will not be exceeded (level of condence) - in N business days?\" The use case: captures an important aspect of risk in a single number easy to understand asks the simple question: \"How bad can things get?" In practice, regulators have traditionally used VaR to calculate the capital they require banks to keep: The market-risk capital has been based on a 10-day VaR estimated where the confidence level is 99%. Credit risk and operational risk capital are based on a one-year 99.9% VaR. Useful measure for liquid positions in normal market conditions over a short period of time. A _ _ VaR IS the loss level that WI\" not be Risk distribution and VAR exceeded with a specified probability. Expected shortfall (E8) is the expected loss (mean) given that the loss is greater than the VaR level (also called C-VaR and Tail Loss). Two portfolios with the same VaR can have very different expected shortfalls. Regulators have indicated that they plan to move from using VaR to using ES for determining market risk capital. - - All outcomes between a loss of $50 million and a gain of $50 million are equally likely for a one-year project. The VaR for a one-year time horizon and a 99% condence level is $49 million. - A one year project has a 98% chance of leading to a gain of $2 million, a 1.5% chance of a loss of $4 million, and a 0.5% chance of a loss of $10 million. The VaR with a 99% confidence level is $4 million. The VaR with a 99.9% confidence level is $10 million. The VaR with a 99.5% condence level is also $10 million. VaR 1055 according to 9899.5% confidence level 0.99 0.935 0.975 0.97 0.965 0.96 [1.955 Loss [5 million) 3 Unti... >