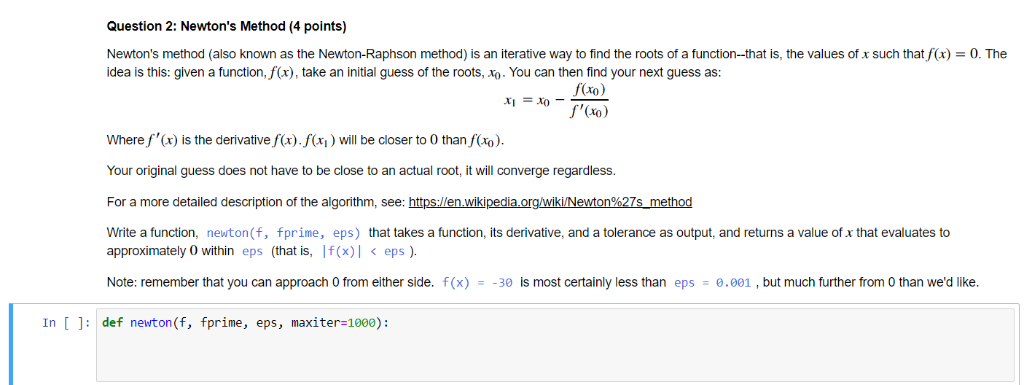
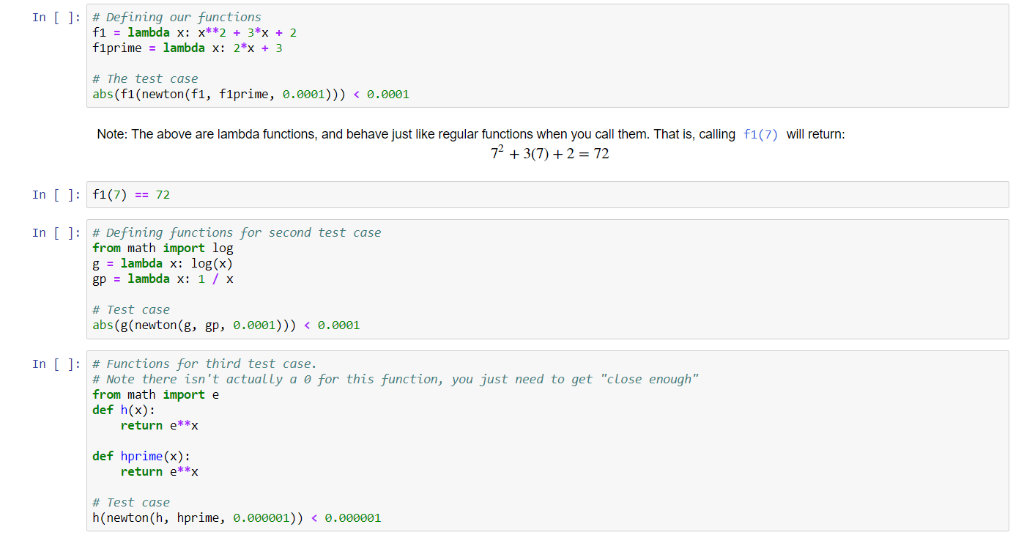
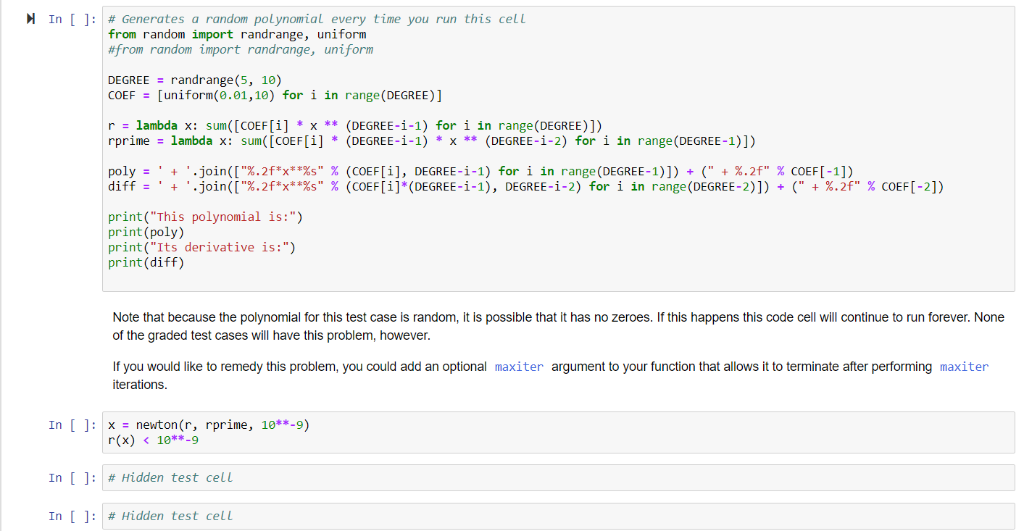
Question 2: Newton's Method (4 points) Newton's method (also known as the Newton-Raphson method) is an iterative way to find the roots of a function-that is, the values of x such that fx)0. The idea is this: given a function, f(x), take an initial guess of the roots, xo. You can then find your next guess as: f (xo) Where f'(x) is the derivat) will be closer to 0 than f Your original guess does not have to be close to an actual root, it will converge regardless. For a more detailed description of the algorithm, see: https:llen wikipedia.org/wikiNewton%27s method Write a function, newton(f, fprime, eps) that takes a function, its derivative, and a tolerance as output, and returns a value of x that evaluates to approximately 0 within eps (that is, If(x)eps) Note: remember that you can approach 0 from either side. f(x)30 is most certainly less than eps .001, but much further from 0 than we'd like. In [ def newton(f, fprime, eps, maxiter-1000): In [ ]: # Defining our functions fiprimelambda x: 2*x +3 # The test case abs (f1 (newton (f1, f1prime, 0.0001))) 0.0001 Note: The above are lambda functions, and behave just like regular functions when you call them. That is, calling f1(7) will return 72 +3(7)+2 72 In [ f1(7)72 In [ ]: # Defining functions for second test case from math import log g lambda x: log(x) gp = lambda x: 1 / x # Test case abs (g (newton (g, gp, 0.0001)))