Question 2. pls answer as soon as you can

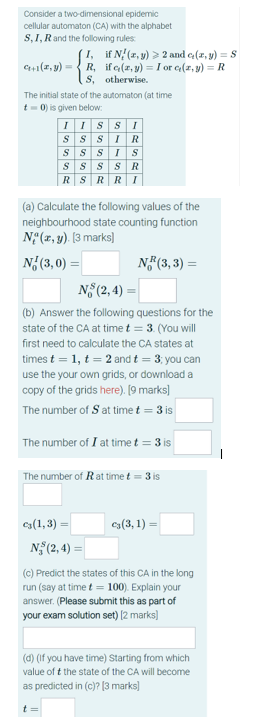
Consider a two-dimensional epidemic cellular automaton (CA) with the alphabet SIR and the following rules 1, if N'(x,y) > 2 and e(t,y) = S C+1(cy) R, if a(x,y= I or c(x,y) = R s, otherwise The initial state of the automaton (at time t - is given below: ITSSI S S SIR SSSTS Sss SR RSRRT (a) Calculate the following values of the neighbourhood state counting function N."(,y). [3 marks] N.(3,0) = N.(3, 3) = N$(2,4) (b) Answer the following questions for the state of the CA at time t = 3. (You will first need to calculate the CA states at timest =1, t = 2 and t = 3: you can use the your own grids, or download a copy of the grids here). (9 marks] The number of Sat time t = 3 is The number of I at time t = 3 is The number of Rat time t = 3 is (1,3) (3,1) N$(2,4) (c) Predict the states of this CA in the long run (say at time t = 100). Explain your answer. (Please submit this as part of your exam solution set) [2 marks] (d) (if you have time) Starting from which value of t the state of the CA will become as predicted in (c)? [3 marks] Consider a two-dimensional epidemic cellular automaton (CA) with the alphabet SIR and the following rules 1, if N'(x,y) > 2 and e(t,y) = S C+1(cy) R, if a(x,y= I or c(x,y) = R s, otherwise The initial state of the automaton (at time t - is given below: ITSSI S S SIR SSSTS Sss SR RSRRT (a) Calculate the following values of the neighbourhood state counting function N."(,y). [3 marks] N.(3,0) = N.(3, 3) = N$(2,4) (b) Answer the following questions for the state of the CA at time t = 3. (You will first need to calculate the CA states at timest =1, t = 2 and t = 3: you can use the your own grids, or download a copy of the grids here). (9 marks] The number of Sat time t = 3 is The number of I at time t = 3 is The number of Rat time t = 3 is (1,3) (3,1) N$(2,4) (c) Predict the states of this CA in the long run (say at time t = 100). Explain your answer. (Please submit this as part of your exam solution set) [2 marks] (d) (if you have time) Starting from which value of t the state of the CA will become as predicted in (c)? [3 marks]