Question 2 requires to derive a conditional probability

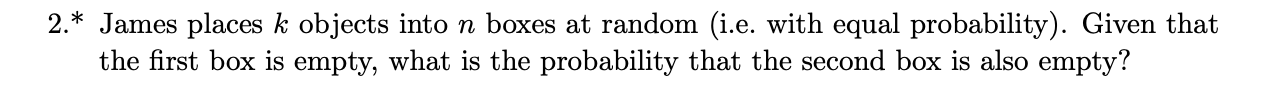
2.* James places k objects into n boxes at random (i.e. with equal probability). Given that the first box is empty, what is the probability that the second box is also empty?3. After many years of happy marriage, Mrs Abdey announces 'I have three children'. (a) Mrs Abdey then says at least two of them are boys. Use Bayes ' theorem to determine the probability that all three of her children are boys. (b) Mrs Abdey then says the two oldest children are boys. Use Bayes' theorem to determine the probability that all three of her children are boys. You may assume that the probability of a birth resulting in a boy is 0.5, and hence also for a girl. You may also assume that the sex of each child is independent. Note you are explicitly asked to use Bayes' theorem to solve this! 4.* A person tried by a three-judge panel is declared guilty if at least two judges cast votes of guilty (i.e. a majority verdict). Suppose that when the defendant is in fact guilty, each judge will independently vote guilty with probability 0.85, whereas when the defendant is in fact not guilty (i.e. innocent), this probability drops to 0.25. If 70% of defendants are guilty, compute the conditional probability that judge number 3 votes guilty given that: (a) judges 1 and 2 vote guilty (b) judges 1 and 2 cast 1 guilty and 1 not guilty vote each (in either order) ((3) judges 1 and 2 both cast not guilty votes