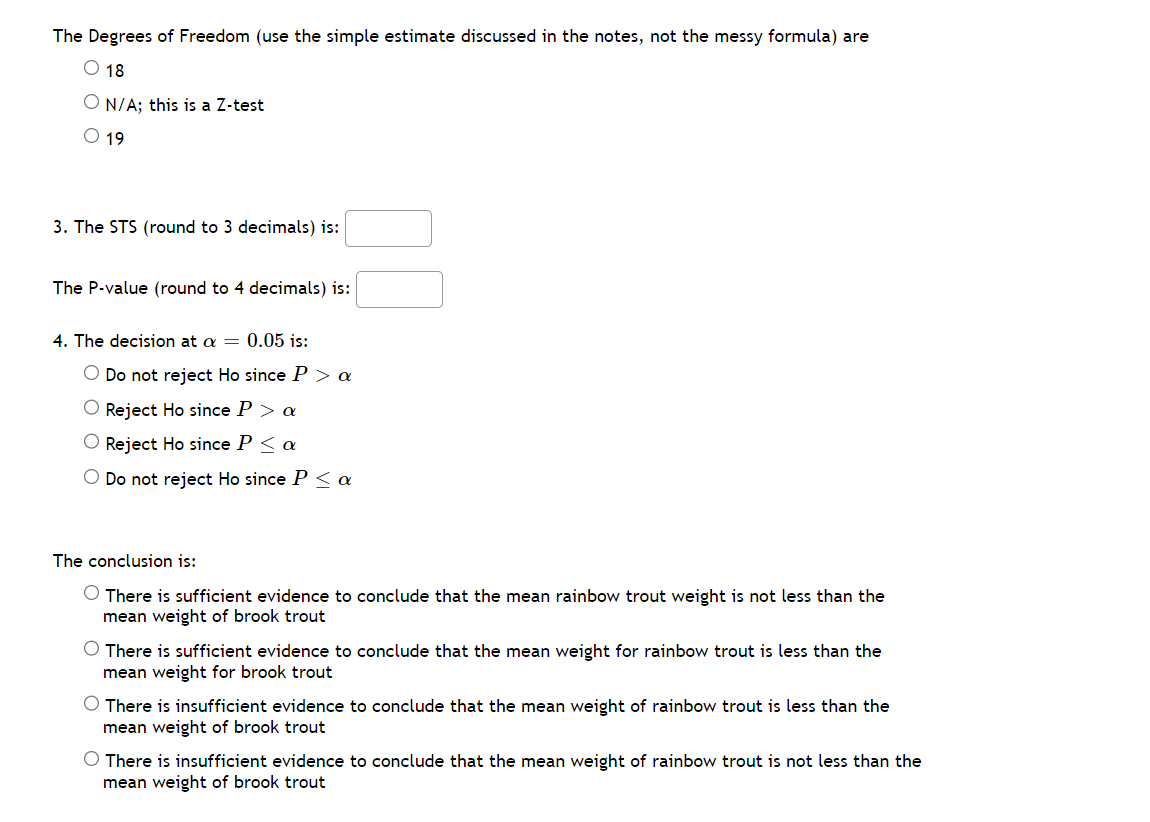
. Question 25 Test the claim that the population mean weight (in pounds) of rainbow trout is less than the population mean weight of brook trout. A random sample of 19 rainbow trout yields a mean weight of 1.21 pounds and standard deviation of 0.3, while a random sample of 20 brook trout yields a mean weight of 1.18 pounds and a standard deviation of 0.5. Use a = 0.05. Let Population 1 be the rainbow trout, and assume that trout weights are normally distributed. 1. The fact that trout weights are normally distributed is important in this test because: O this is a T-test O this is a Z-test O both sample means are less than thirty O both sample sizes are less than thirty The hypotheses are: O Ho: P1 P2 O Ho: M1 = 12; Ha: M1 # 12 O Ho:P1 = p2; Ha: p1 # P2 O Ho: P1 2 P2; Ha : P1 M2 O Ho: M1 2 12; Ha: H1 or C' Reject Ho since P :3 or C' Reject Ho since P g or '33:? Do not reject Ho since P 3' or The conclusion is: '33:} There is sufficient evidence to conclude that the mean rainbow trout weight is not less than the mean weight of brook trout '3' There is sufficient evidence to conclude that the mean weight for rainbow trout is less than the mean weight for brook trout '3' There is insufficient evidence to conclude that the mean weight of rainbow trout is less than the mean weight of brook trout '33:? There is insufficient evidence to conclude that the mean weight of rainbow trout is not less than the mean weight of brook trout