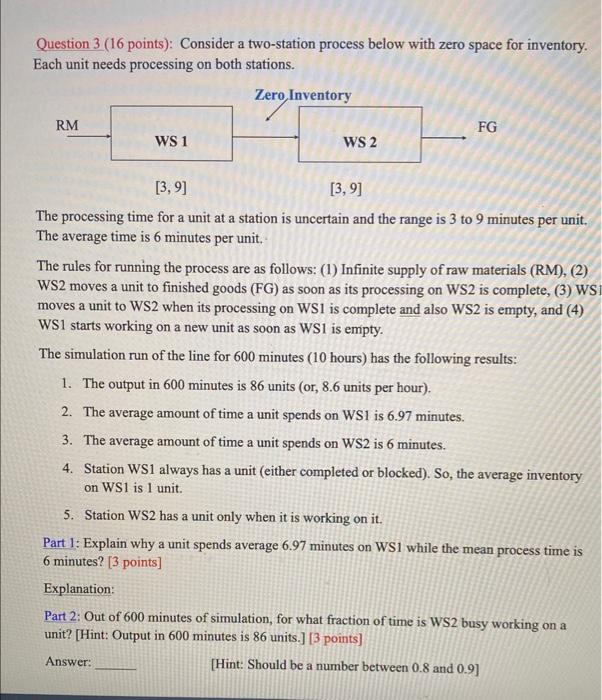
Question 3 (16 points): Consider a two-station process below with zero space for inventory. Each unit needs processing on both stations. The processing time for a unit at a station is uncertain and the range is 3 to 9 minutes per unit. The average time is 6 minutes per unit. The rules for running the process are as follows: (1) Infinite supply of raw materials (RM), (2) WS2 moves a unit to finished goods (FG) as soon as its processing on WS2 is complete, (3) WS moves a unit to WS2 when its processing on WS1 is complete and also WS2 is empty, and (4) WS1 starts working on a new unit as soon as WS1 is empty. The simulation run of the line for 600 minutes ( 10 hours) has the following results: 1. The output in 600 minutes is 86 units (or, 8.6 units per hour). 2. The average amount of time a unit spends on WS1 is 6.97 minutes. 3. The average amount of time a unit spends on WS 2 is 6 minutes. 4. Station WS1 always has a unit (either completed or blocked). So, the average inventory on WS1 is 1 unit. 5. Station WS2 has a unit only when it is working on it. Part 1: Explain why a unit spends average 6.97 minutes on WS1 while the mean process time is 6 minutes? [3 points] Explanation: Part 2: Out of 600 minutes of simulation, for what fraction of time is WS2 busy working on a unit? [Hint: Output in 600 minutes is 86 units.] [ 3 points] Answer: [Hint: Should be a number between 0.8 and 0.9 ] Part 3: Justify that the total inventory in the process (sum for WS1 and WS2) is 1.86. Justification: [ 3 points] Part 4: Using the total inventory from Part 3 and the flow rate of 8.6/60 units per minute, calculate the flow time using Little's Law. [7 points] Answer: [Hint: 12 or more] Work