Question: Question 3 (2 points) Let T : P2(R) R be a linear transformation such that ker(T) = [p(t) e %3D P2 (IR): p'(1) = 0},
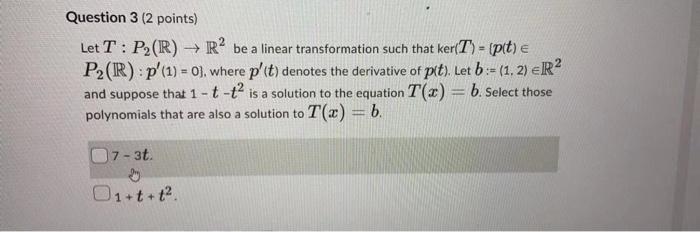
Question 3 (2 points) Let T : P2(R) R2 be a linear transformation such that ker(T) = (pit) e P2(R): p'(1) = 0), where p't) denotes the derivative of pit). Let b := (1, 2) eR2 and suppose that 1 - t-t is a solution to the equation T(x) = 6. Select those polynomials that are also a solution to T(x) = b. 17-3t. On+t+t
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


