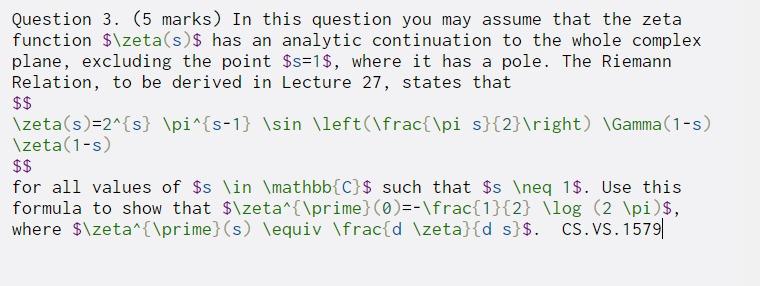
Question 3. (5 marks) In this question you may assume that the zeta function $\zeta(s)$ has an analytic continuation to the whole complex plane, excluding the point $s=1$, where it has a pole. The Riemann Relation, to be derived in Lecture 27, states that $$ Izeta(s)=2^{s} \pi^{s-1} \sin \left(\frac{\pi s}{2} ight) \Gamma(1-5) Izeta (1-3) $$ for all values of $s \in \mathbb{C} $ such that $s eq 1$. Use this formula to show that $\zeta^{\prime} ( )=-\frac{1}{2} \log (2 \pi $, where $\zeta^{\prime} (s) \equiv \frac{d \zeta}{d s}$. CS.VS. 1579|| $