Question: Question 3 (5 points). Let f be an entire function whose real part Re f has an upper bound, that is for all 2: we

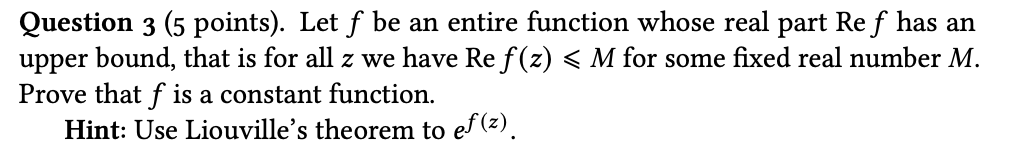
Question 3 (5 points). Let f be an entire function whose real part Re f has an upper bound, that is for all 2: we have Re f (z) s M for some xed real number M. Prove that f is a constant function. Hint: Use Liouville's theorem to 6\"\

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

lathu2nd please answer all in step by step manner. please dont give wrong answer. thank you. q1: Formulas: x-bar i m phat 1r m estimate i m phat = x I n p = X I N x-bar i T (s 1 xi?) p-hat i z \\l...

M New OTP for aut X MY SCF Home: S X Study Guide 1: B X Section 5.6 X Do Homework - X *Dashboard X Mathway | Precal X C Chegg Search re: X + X C @...

Need to fill in all parts that say "Implement me" and answer in one or two lines here. The following cell contains code that will be referred to as the Preprocessing Block from now on. It contains a...

This week?s assignment is the fourth short paper component of our Return on Investment (ROI) project. The focus of this week?s writing will be to consider the value and steps necessary in preparing a...

the problems are attached below. e] Prim-ride a restriction on parameter values such that a steady state equilibrium pair {11:13] exists. Is it unique?. {No need for a lengthy discussion} f] What is...

Macro...solve all the following 1.5 Options 1. A stock price is currently $50. It is known that at the end of two months it will be either $53 or $48. The risk-free interest rate is 10% per annum...

Analyze the following questions and answer all. Scenario: Imagine you are a business consultant to a firm of your choice. You have been asked to analyze, advise, and create recommendations on how the...

Please help Question 3 (20 points) Consider the standard growth model in discrete time. There is a large number of identical households normalized to 1. Each household maximizea life-time discounted...

Unit 2 Progress Check: FRQ Part A Submit X 1 Unit 2 Progress Check: FRQ Part A Question 1 A GRAPHING CALCULATOR IS REQUIRED FOR THIS QUESTION. Submit 1 of 1 x You are permitted to use your calculator...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

What are quality improvement programs?

On May 10, Tharp Corporation issues 2,500 shares of $5 par value common stock for cash at $13 per share. Journalize the issuance of the stock.

10 Here are some expression cards. Sort the cards into groups of equivalent expressions. A 8y(5+6y) B 4y(5y+6y) C 2y(24y+20) D 2y2(10+12y) LU E 4(10y+12y) F 4y(6y+5) G y(20+24y) H y(40+48y)

On 1 March 2007 DB Limited issued R560 000 15% debentures at R98. The debentures were to be redeemed at par in four equal annual payments starting 28 February 2010. Required: Journalise the above...